cs
- 08.Advanved Search Trees.pdf P43
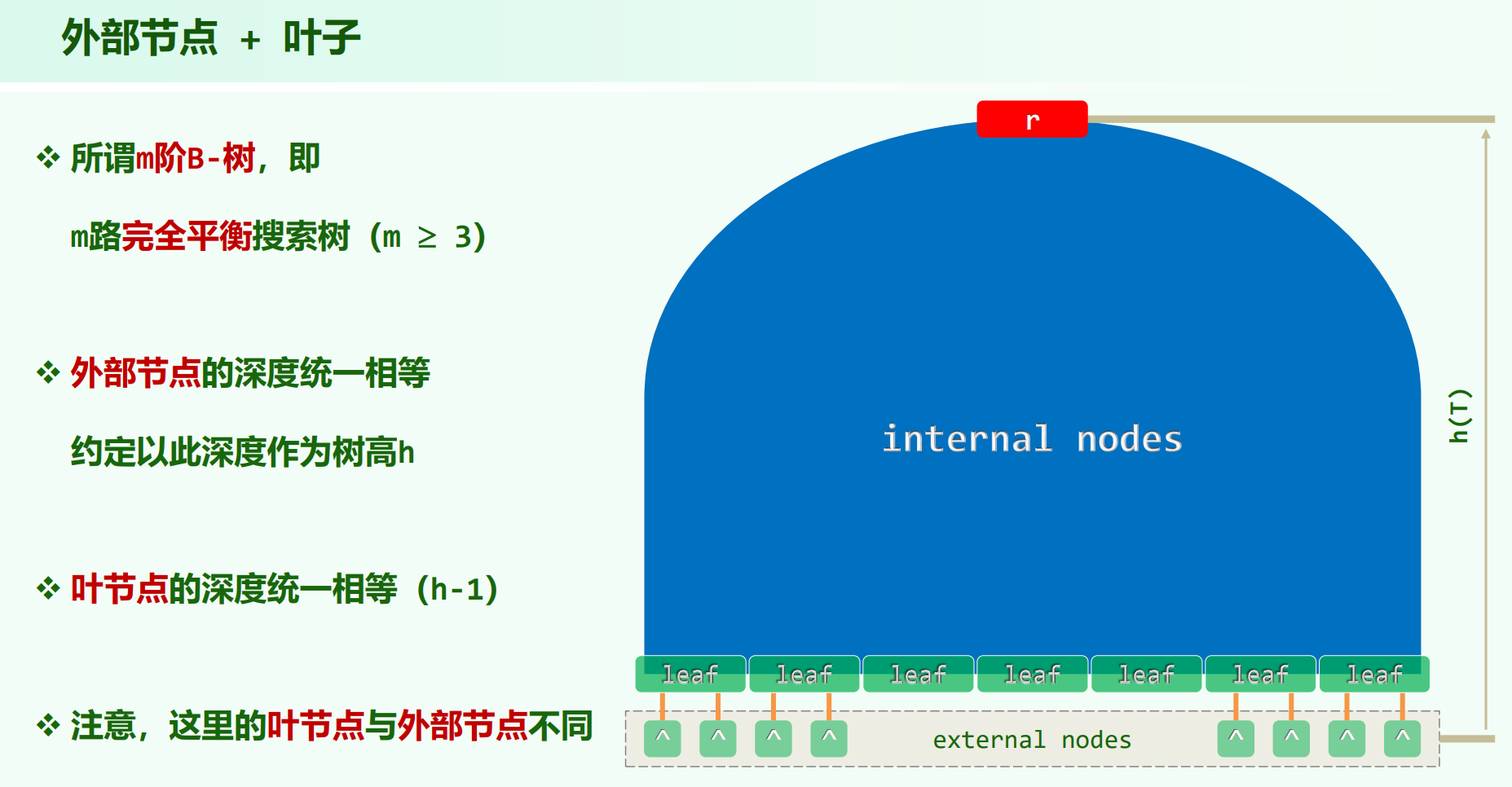
B树的高度要算外部节点,叶节点是指外部节点上一层的节点,B树的特性,叶节点都会在 h - 1 深度的位置。
外部节点相对的就是内部节点,所以内部节点包含叶节点。
节点关键码与分支数
每个内部节点有 $n$ 个关键码,$n + 1$ 个分支。对于m阶B树,需要满足:
内部节点:$n + 1 \le m$
反过来,分支数也不能太少
根:$n + 1 \ge 2$,也就是根特殊,最少可以只有 $1$ 个关键码
根以外的内部节点:$n + 1 \ge \lceil m / 2 \rceil$
m阶B-树也称 $(\lceil m / 2 \rceil, m)$-树(这两个数字是内部节点分支数,根要例外,根分支数可以小到 $2$ ,$1$ 个关键码)。
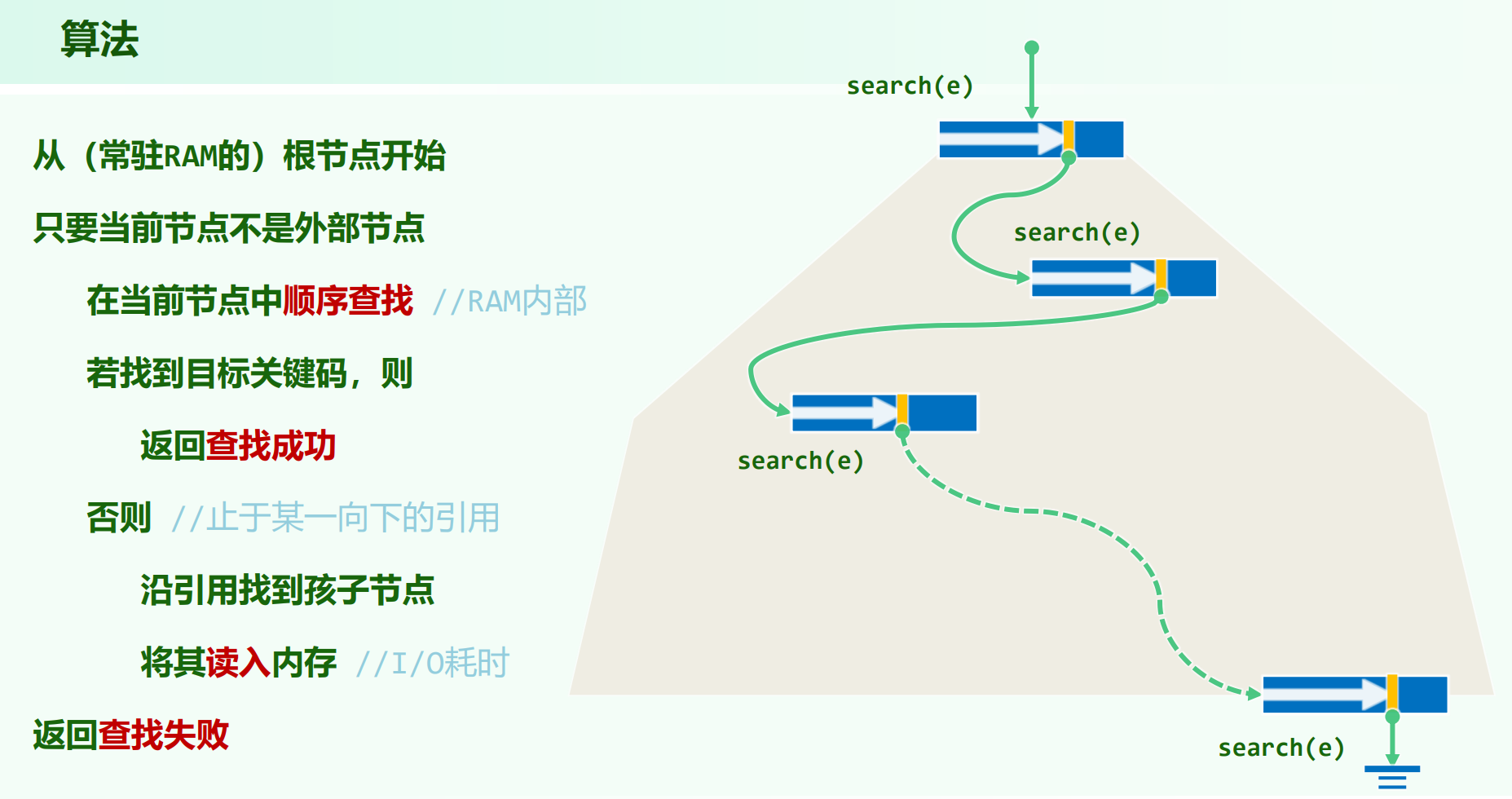
B树的I/O
根节点默认在内存。
B树高度
记 $N$ 个关键码的 $m$ 阶B-树的高度为 $h$,则有:
\[log_m(N + 1) \le h \le 1 + log_{\lceil \frac{m}{2} \rceil}\frac{N + 1}{2}\]证明:
每层关键码取最少,也即分支数最少,以使树最高,每层节点数为:
$n_0 = 1$
$n_1 = 2$
$n_2 = 2 \times \lceil \frac{m}{2} \rceil$
$n_3 = 2 \times \lceil \frac{m}{2} \rceil^2$
$…$
$n_h = 2 \times \lceil \frac{m}{2} \rceil^{h - 1}$
第 $h$ 层为外部节点,对应查找失败的情况,外部节点数 = 关键码数 + 1,所以 $N + 1 \ge 2 \times \lceil \frac{m}{2} \rceil^{h - 1}$ ,得到 $h$ 上界。
关键在于要用外部节点数 = 关键码数 + 1,所以要分析外部节点数,而非去分析每层关键码数(分析这个会很麻烦)。
每层关键码取最多,也即分支数最多,以使树最矮,每层节点数为:
$n_0 = 1$
$n_1 = m$
$…$
$n_h = m^h$
同理,第 $h$ 层为外部节点,$N + 1 \le m^h$ ,所以 $log_m{(N + 1)} \le h$
B树的高度为 $\Theta(log_m{N})$ 。
插入
除根以外,每个内部节点关键码个数范围 $[\lceil \frac{m}{2} \rceil - 1, m - 1]$ 。
插入一定会插到叶节点里。
若插入后关键码太多($m$ 个)上溢,则要进行分裂,选下标为 $s = \lfloor \frac{m}{2} \rfloor$ 处的关键码(正中(奇数)或正中偏右(偶数)),将 $k_s$ 上升一层到父节点中,以分裂所得的两个节点为 $k_s$ 的左右孩子(左右孩子的关键码数一定会是合法的)。
上溢可能向上传播,若上溢传播到根节点,则被提升的关键码自成一个节点,成为新树根。这是B树长高的唯一可能。
删除
除根以外,每个内部节点关键码个数范围 $[\lceil \frac{m}{2} \rceil - 1, m - 1]$ 。
B树的非叶节点的内部节点一定是多分支的,不可能存在单分支的情况。
若删除的关键码所在节点非叶节点,则关键码的直接后继一定在叶节点中(若不在叶节点中,则继续走左分支能找到更小的)。将其与直接后继交换,在叶节点上删除。
删除之后可能关键码太少($\lceil \frac{m}{2} \rceil - 2$ 个)下溢,
-
若下溢节点没有兄弟,则说明其一定为根节点,根节点的关键码最少可以只有 $1$ 个,若这还下溢了,说明根节点变空了,要选儿子为新根或者B树已为空树。(在教材P224代码里这是递归基,会先判断当前节点是否下溢,是否为根,代码上不会真正遇到需要处理左右孩子都为空的情况)
-
若下溢节点有兄弟,看其关键码数够不够借,
2.1 若左/右兄弟之一的关键码数 $\ge \lceil \frac{m}{2} \rceil$ 个(够借)。
用兄弟右/左边缘的那个关键码 $x$,和父节点中的对应关键码 $y$ 做一次旋转,$y$ 进来补下溢,$x$ 上去接替 $y$。这样满足了搜索树的顺序性,下溢修复完毕。
2.2 若左右兄弟都不够借。
则左右兄弟或不存在,或其关键码数为 $\lceil \frac{m}{2} \rceil - 1$ ,但至少有一个兄弟。通过父节点中对应的节点,将下溢节点与兄弟粘接。新生成的节点关键码数为 $2 \cdot \lceil \frac{m}{2} \rceil - 2$ ,一定合法。由于父节点少了一个节点,下溢可能向上传播,若传播到根,则根节点要废弃,选儿子为新根。这是B树变矮的唯一可能。
例子
插入:08.Advanved Search Trees.pdf P63
删除:08.Advanved Search Trees.pdf P73