cs
桶排序
MaxGap问题
用桶把 $n$ 个数分为大约 $n$ 个段
还有道用桶的:LeetCode220. 存在重复元素 III
时间复杂度:$O(n + M)$ ,$n$ 为数字个数,$M$ 为值域范围。
基数排序
数字个数为 $n$ ,$M$ 为值域范围
时间复杂度为:$O(log_{10}M \cdot (n + 10))$
$log_{10}M$ 代表位数,如果 $M$ 不能视为常数,例如是 $\Theta(n)$ 规模的,则总时间复杂度不能视为常数。
09.Dictionary.pdf P75 弄了这样一个优化:

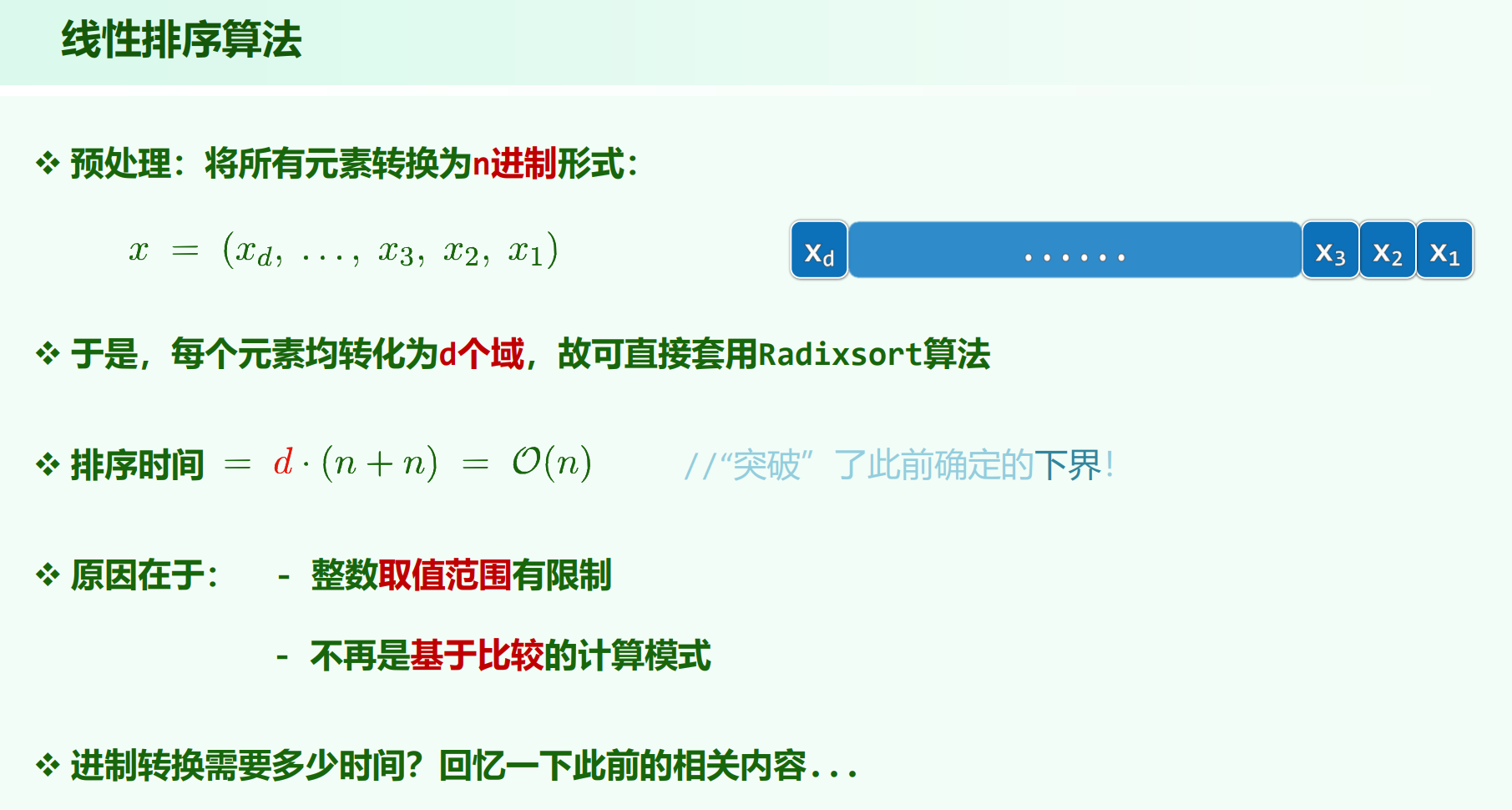
把元素转换为 $n$ 进制,转换后的数字的位长为 $log_nM$ ,每位的数字范围为 $0 \sim n - 1$。一个元素的进制转化时间为 $O(log_nM)$ ,总的进制转化时间为 $O(nlog_nM)$
则时间复杂度为 $O(nlog_nM + log_nM \cdot (n + n))$
在何种约束下是线性的?
$log_nM$ 为常数时,即 $M = O(n^d)$ 时,$d$ 为某个常数。这也就是ppt上说的对数密度 $\frac{lnn}{lnM} = \frac{1}{d} = O(1)$ 。
使用转成 $n$ 进制的方法,只要 $M$ 还在 $n$ 的多项式范围内,就可以认为基数排序的时间复杂度为线性的。
如果 $M$ 更大例如 $M = n^n$ 之类的,那么时间复杂度就不是线性的了。
(但是实际这样做应该没什么用,看似无代价地把大数 $n$ 放到了底数位置,但 $n$ 真的够大的话,转成 $n$ 进制后的每一位的长度就不能视为 $O(1)$ 了,而是 $log_2{n}$。整体还该有个 $log_2{n}$ 的倍数,$log_nM \cdot (n + n) \cdot log_{10}n = log_{10}M \cdot (n + n)$ ,没什么变化)
计数排序
记值的出现频率,求频率的前缀和,然后从右到左遍历输入序列,根据频率的前缀和确定每个元素的排序后位置。
从右到左遍历输入序列是为了排序稳定性,从左到右的话大小顺序能对,但是不稳定。