cs
04.Stack + Queue.pdf P67
栈混洗
$n$ 个元素的栈混洗。
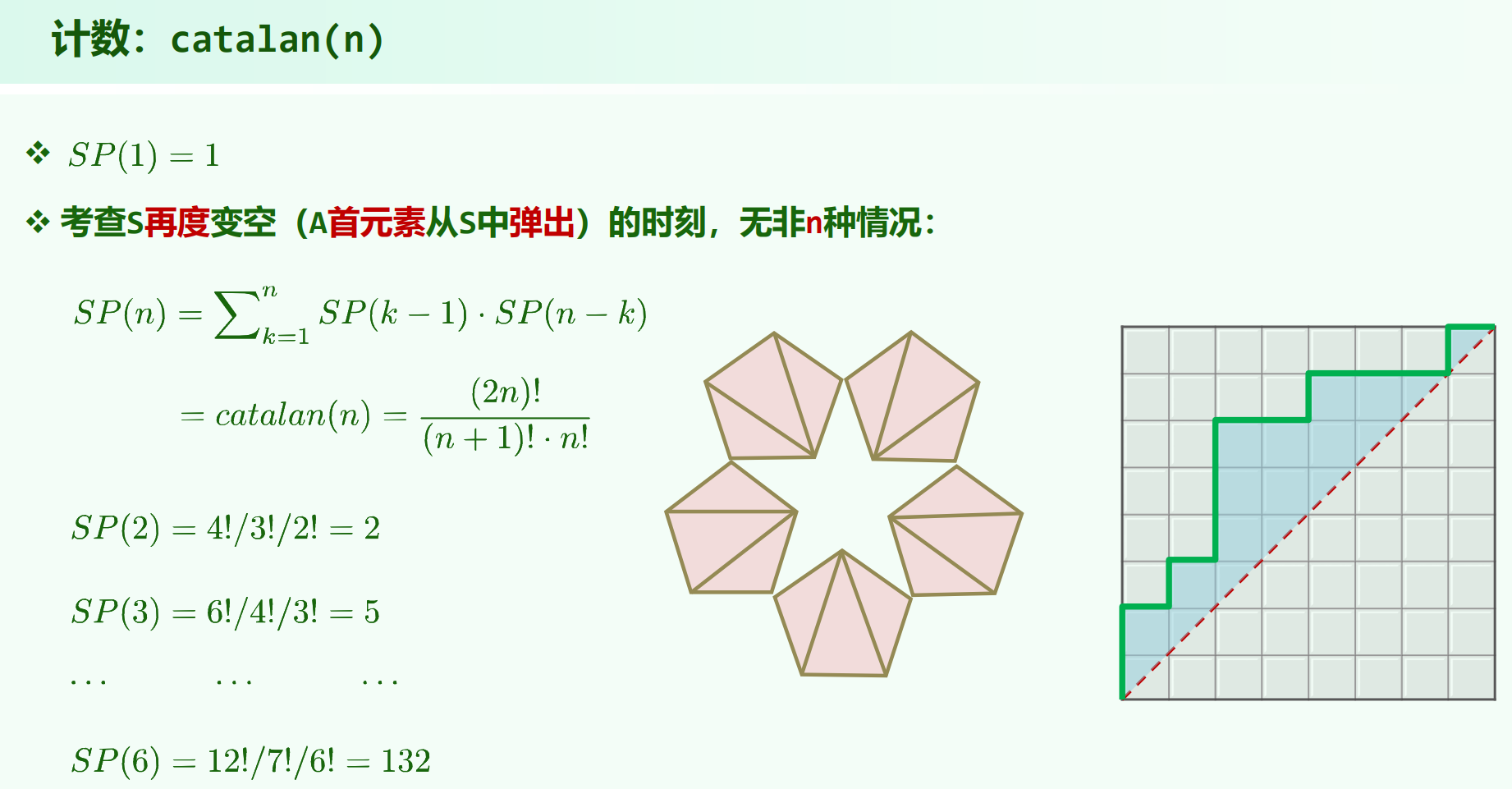
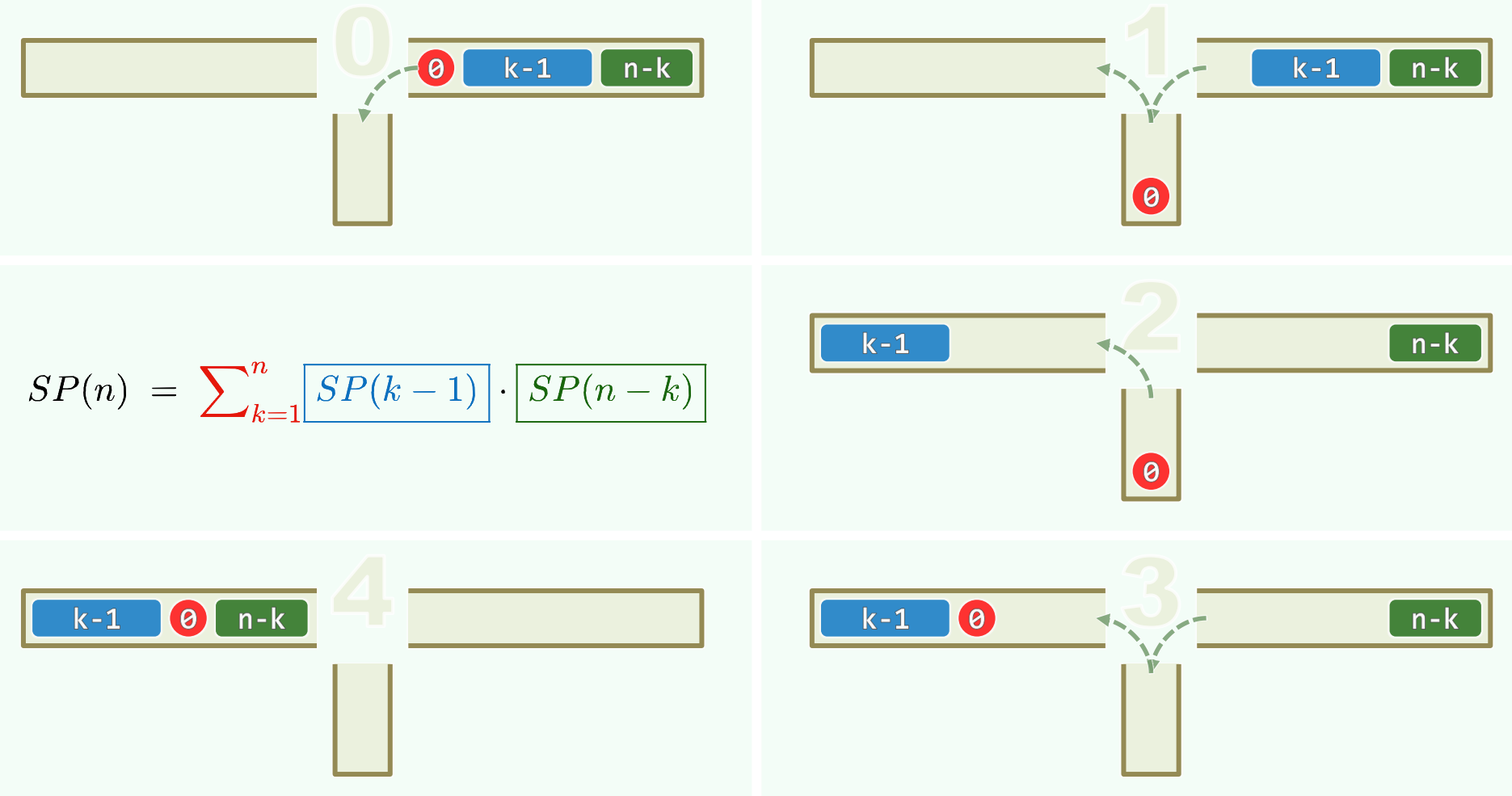
考虑第一个元素入栈后到出栈的这段时间,中间经过了一段元素的栈混洗,长度从 $0$ 到 $n - 1$,也就是说,可以将原序列分为长为 $1, k - 1, n - k$ 的三段。被第一个元素的出栈分隔为了两部分独立的子栈混洗问题。所以:
$ SP(n) = \sum \limits_{k = 1}^{n} SP(k - 1) \cdot SP(n - k) $
这个递推式为 $catalan数$ ,通式为:
$ catalan(n) = \binom{2n}{n} - \binom{2n}{n-1} = \frac{1}{n + 1}\ C_{2n}^{n} $
禁形
习题解析[4-3]
原序列的 i … j … k 不可能经栈混洗后变成 k … i … j 的形式,这种形式称为禁形。
禁形 和 序列为非法栈混洗 是充要的,见习题解析[4-3]。
不过习题解析其实并没有证明:“没有禁形,序列一定合法” 这一点,只是口头说了下没有禁形那个代码一定不会有问题。这里证明下:
从原序列第一个元素的出栈入手,把原序列分为长为 $1, k - 1, n - k$ 的三段。由于整体没有禁形,则 $[k - 1]$段 和 $[n - k]$段 在输出序列中各自也没有禁形,二者由归纳假设可以栈混洗,再考虑第一个元素,由于 $ 1, [k - 1], [n - k] $ 在输出序列中也必不是禁形的形式,所以第一个元素能正常出入栈,并将两段分割成独立的子问题。证明完毕。
相关题目: LeetCode946. 验证栈序列
禁形的等价形式
习题解析[4-3]b
$k … i … j$ 式禁形和 $(j + 1) … i … j$ 式禁形是完全等价的。
若序列存在 $(j + 1) … i … j$ 禁形,则显然取 $k = j + 1$ 就是 $k … i … j$ 禁形。只需证明:
若序列存在 $k … i … j$ 禁形,则一定存在 $(j + 1) … i … j$ 禁形。(注意前后者的 i, j 并不一定相等,后者其实是指 $(j’ + 1) … i’ … j’$)
-
若 $k = j + 1$ ,则 $k … i … j$ 就是后者式禁形,成立
-
若 $k > j + 1$ ,考虑 $k - 1 (> j)$ 所在的位置与 $i$ 的关系,
-
$k - 1$ 在 $i$ 的左边,$(k - 1) … i … j$ ,忽略掉其中可能含有的 $k$,这相当于是一个原序列 $i … j … (k - 1)$ 的排列结果,现在已经出现了禁形形式1 ((k - 1) … i … j),可以归纳证明其一定会出现禁形形式2。
-
$k - 1$ 在 $i$ 的右边,则 $k … i … (k - 1)$ 就是一个禁形形式2。
-
综上,序列含有禁形形式1 等价于 序列含有禁形形式2。对于判断序列是否为合法的栈混洗,可以用禁形形式2得到一个做法:
从左到右遍历一遍待判断的序列,例如现在遍历到 $i$ ,那么在 $i$ 的右侧找原序列中 $i$ 的直接前驱 $’ i - 1 ‘$,然后看二者之间是否夹了更前驱的元素。对每个 $i$ 都没有 $\iff$ 原序列合法。
补充ppt(答案是C,”CAB”是禁形形式2):

当然,用LeetCode946. 验证栈序列的方式更正规。
catalan数的多种形式
-
$n$ 个元素的栈混洗
-
$n$ 个左括号 和 $n$ 个右括号组成的合法匹配的方案数
注意是 $n$ 对匹配的括号,一共有 $2n$ 个字符
-
$n + 1$ 个数字连乘,不同的计算顺序个数
相当于加入 $n$ 对合法括号
-
$n$ 个节点的二叉树可能的形态数
$f(n) = f(0)f(n-1) + f(1)f(n-2) + … + f(n-1)f(0)$
-
有 $n$ 个非叶节点的真二叉树的可能形态数
选一个节点为根,左侧有 $i$ 个非叶节点,右侧有 $n - 1 - i$ 个非叶节点。
相当于 4 的情况给每个节点补成有2个孩子(如果需要补的话)
-
$n$ 个节点的二叉搜索树的形态数 ($n$ 个节点互异的二叉搜索树的种类)
只是形态,和 4 是一样的。然后知道形态后,数字放进去的结尾是确定的,也可以直接哪个数字做根,然后写递推式。
-
$n$ 个叶节点的真二叉树的形态数是 $catalan(n - 1)$
对任意二叉树,$n_0 = n_2 + 1$ ,再用 5
-
边长度为 $n \times n$ 的格点,不走到右下区域(可以在对角线上),从左下走到右上的种数
任意时刻向上的步数 >= 向右的步数,这和栈混洗栈总要有东西才能出栈是一样的。
-
$2n$ 个数,其中有 $n$ 个 $1$ 和 $n$ 个 $-1$ ,从左到右扫描,$1$ 的累计个数总是不小于 $-1$ 的累计个数的排列数
$1$ 和 $-1$ 与栈混洗的入栈出栈是对应的,$1$ 的累计个数 >= $-1$ 的累计个数,对应栈混洗总要有东西才能出栈。
-
将一个 $n + 2$ 条边的凸多边形分割为三角形的方案数 (多边形三角剖分数)
选一条固定边作为基础,然后考虑另外一个点的位置
$f(n + 2) = \sum \limits_{k = 2}^{n + 1} f(k) \cdot f(n + 3 - k),f(3) = 1,f(2) = 0$
令 $g(n) = f(n + 2)$,则 $g(n) = \sum \limits_{k = 2}^{n + 1} g(k - 2) \cdot g(n - k + 1) = \sum \limits_{k = 1}^{n} g(k - 1) \cdot g(n - k),g(1) = 1,g(0) = 0$。所以 $g(n) = catalan(n)$,$f(n + 2) = catalan(n)$
-
在圆上有 $2n$ 个点,连接这些点形成 $n$ 条不相交弦的方案数 (不相交弦问题)
由于要把所有点连成不相交弦,所以划分时左右都是偶数个点,$2k$ 个点的方案数记为 $f(k)$ ,然后写递推式。
这两条来自链接。
递推式到通式的证明
法一:反射定理
用形式9,$n$ 个 $1$ 和 $n$ 个 $-1$,总排列方案数为 $C_{2n}^{n}$,再排除非法方案。
这里先说明一下形式9的等价定义,最开始位于 $(0, 0)$,每步要么移动 $(1, 1)$ (对应 $1$),要么移动 $(1, -1)$ (对应 $-1$)。由于 $1$ 和 $-1$ 的个数都为 $n$,最后会到达 $(2n, 0)$。$catalan(n)$ 为这种定义下,过程中 $y$ 始终 $\ge0$ 的方案数。
对于非法方案,其至少存在一个位置 $k$,使得此处 $-1$ 的个数比 $1$ 多 $1$。由于 $1$ 和 $-1$ 都是 $n$ 个,所以右侧还有 $x + 1$ 个 $1$ 和 $x - 1$ 个 $-1$。把右侧的 $1$ 和 $-1$ 反转,序列变成了 $n + 1$ 个 $-1$ 和 $n - 1$ 个 $1$ 的排列。反过来,一个$n + 1$ 个 $-1$ 和 $n - 1$ 个 $1$ 的排列,其最终会到达 $(2n, -2)$ ,用介值定理,一定有一个点是 $(x, -1)$,此时 $-1$ 恰比 $1$ 多一个,将右侧的 $1$ 和 $-1$ 反转,排列变成了一种 $n$ 个 $1$ 和 $n$ 个 $-1$ 的非法方案。
所以,“$n + 1$ 个 $-1$ 和 $n - 1$ 个 $1$ 的排列” 和 “$n$ 个 $1$ 和 $n$ 个 $-1$ 的所有非法方案” 是一一对应的。
所以,非法方案总数为 $C_{2n}^{n-1}$。
$ catalan(n) = C_{2n}^{n} - C_{2n}^{n-1} = \frac{1}{n + 1}\ C_{2n}^{n} $
扩展问题
上面的链接里给出了更一般的结论:
$b_0 > 0, b_n > 0$ 且 $(a, b_0)$ 与 $(a + n, b_n)$ 确实可以用斜率为 $+1 / -1$ 的折线到达,则:
-
连接格点 $(a, b_0)$ 与 $(a + n, b_n)$ 且与x轴有公共点的折线条数为 $C_{n}^{\frac{1}{2}(n + b_n + b_0)}$
问题是等价于 $n$ 步 $+1 / -1$ , 从 $(a, -b_0)$ 到 $(a + n, b_n)$ 的方案数。因为与x轴有交点,一定可以用最靠左的那个交点把 $(a, b_0)$ 视作 $(a, -b_0)$;反过来,以 $(a, -b_0)$ 为起点,一定会与x轴相交。所以是充要的。

-
连接格点 $(a, b_0)$ 与 $(a + n, b_n)$ 且与x轴没有公共点的折线条数为 $C_{n}^{\frac{1}{2}(n + b_n - b_0)} - C_{n}^{\frac{1}{2}(n + b_n + b_0)}$
总方案数 - 非法方案数
(注意以上的 2 是严格 $ > 0 $。)
此外,只要问题输入没问题,那么一定有 $\frac{1}{2}(n + b_n + b_0)$ 为偶数,因为:
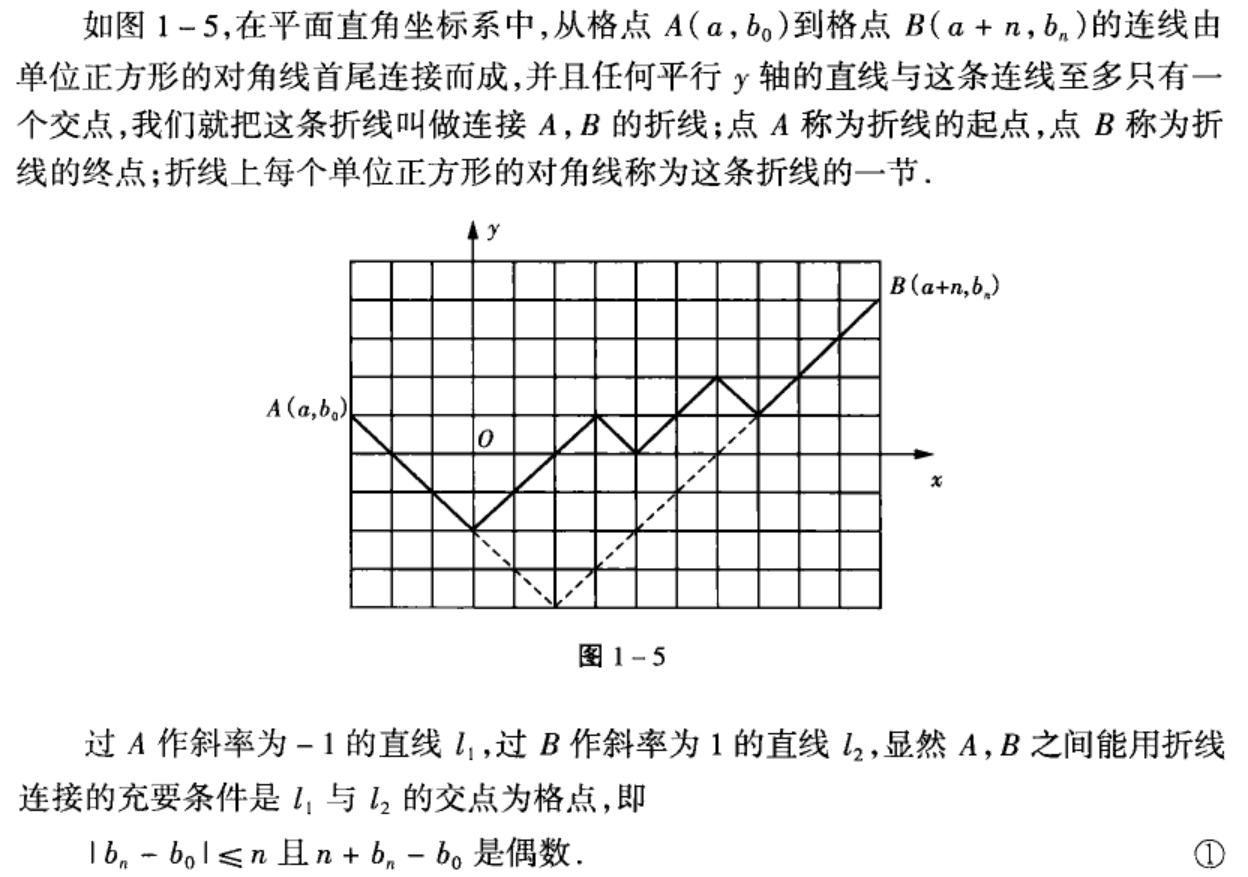
现在用这个更一般的结论来求 $catalan(n)$:
$catalan(n)$ 相当于从 $(0, 0)$ 走到 $(2n, 0)$,$y$ 始终 $> -1$,相当于从 $(0, 1)$ 走到 $(2n, 1)$,$y$ 始终 $> 0$,带进上面的结论2,结果就是 $C_{2n}^{n} - C_{2n}^{n + 1}$
还有个比较有意思的数学代换是:由于最开始和末尾都有 $y = 0$ ,要始终 $y \ge 0$ ,那么第一步肯定是 $+1$ ,最后一步肯定是 $-1$ 。问题相当于 $(1, 1)$ 走到 $(2n - 1, 1)$,$y$ 始终 $> -1$,带进上面的结论2,结果是 $C_{2n - 2}^{n - 1} - C_{2n - 2}^{n + 1}$,看起来和 $C_{2n}^{n} - C_{2n}^{n + 1}$ 不像,但是代换之后实际是相等的。$C_{2n - 2}^{n - 1} - C_{2n - 2}^{n + 1} = (2n - 2)! \frac{2(2n - 1)}{(n + 1)! (n - 1)!} = \frac{(2n)!}{(n + 1)!n!} = catalan(n)$
为什么 $C_{2n - 2}^{n - 1} - C_{2n - 2}^{n + 1} = C_{2n}^{n} - C_{2n}^{n + 1}$ ?
首先,$C_{n}^{m} = C_{n - 1}^{m} + C_{n - 1}^{m - 1}$ (证明: n个球里选m个,分第一个球选/不选即可)
利用这个公式把2n往2n-2靠,右 = $C_{2n - 1}^{n} + C_{2n - 1}^{n - 1} - (C_{2n - 1}^{n + 1} + C_{2n - 1}^{n}) = C_{2n - 1}^{n - 1} - C_{2n - 1}^{n + 1}$
再做一步这个,然后结合 $C_{2n - 2}^{n - 2} = C_{2n - 2}^{n}$ 就可以得到上面的式子了。
法二:生成函数法
https://oi-wiki.org/math/poly/ogf/
https://oi-wiki.org/math/combinatorics/catalan/#%E5%B0%81%E9%97%AD%E5%BD%A2%E5%BC%8F
用 $h_n$ 记 $catalan(n)$
令生成函数 $g(x) = h_0 + h_1x + h_2x^2 + h_3x^3 + … + h_nx^n + …$ ,即把要求的通项作为一个幂级数的系数
(注意 $h_0$ 是等于 $1$ 的。 (OEIS))
然后把 $g(x)$ 平方,得到 $g(x)^2 = h_0^2 + (h_0h_1 + h_1h_0)x + (h_0h_2 + h_1h_1 + h_2h_0)x^2 + … + (h_0h_n + h_1h_{n-1} + h_2h_{n-2} + … + h_nh_0)x^n + … = \sum \limits_{n = 0}^{\infty}(\sum \limits_{i = 0}^{n}h_ih_{n-i})x^n$。
(平方系数会出现卷积,这是柯西乘积(Cauchy product))
$ SP(n) = \sum \limits_{k = 1}^{n} SP(k - 1) \cdot SP(n - k) $,即 $ h_n = \sum \limits_{k = 1}^{n} h_{k-1} \cdot h_{n - k} $,那么 $h_{n+1} = \sum \limits_{k = 1}^{n + 1} h_{k-1} \cdot h_{n + 1 - k} = \sum \limits_{k = 0}^{n} h_{k} \cdot h_{n - k}$
所以,$g(x)^2 = h_1 + h_2x + h_3x^2 + …$,所以,$xg(x)^2 = g(x) - 1$,解得 $g(x) = \frac{1 - \sqrt{1 - 4x}}{2x}$ (取减号的那个解,因为将其分子有理化后符合 $h_0 = 1$),
然后,$(1 + x)^\alpha = \sum \limits_{k = 0}^{\infty} \binom{\alpha}{k}x^k$ ,现在先证:
对于 $k \ge 1$ ,
\[\binom{\frac{1}{2}}{k}(-4)^k = -\frac{\binom{2k}{k}}{2k - 1}\]由于
\[\binom{\frac{1}{2}}{k} = \frac{(1/2)(1/2 - 1)...(1/2 - k + 1)}{k!} = (-1)^{k-1}\frac{(2k - 3)!!}{2^kk!}\]所以
\[\binom{\frac{1}{2}}{k}(-4)^k = -\frac{2^k(2k - 3)!!}{k!} = -\frac{2^k(2k-3)!}{k!(2k-4)(2k-6)...2}\]而 $(2k-4)(2k-6)…2 = 2^{k-2}(k-2)!$,故
\[\begin{align*} =& -\frac{2^k(2k-3)!}{k!2^{k-2}(k-2)!} \\ =& -\frac{4(2k-3)!}{k!(k-2)!} \\ =& -\frac{4(2k)!}{k!(2k)(2k-1)(2k-2)(k-2)!} \\ =& -\frac{(2k)!}{k!k(2k-1)(k-1)(k-2)!} \\ =& -\frac{1}{2k-1}\frac{(2k)!}{k!k!} \\ =& -\frac{\binom{2k}{k}}{2k - 1} \end{align*}\],得证。
故
\[\sqrt{1-4x} = 1 + \sum \limits_{k = 1}^{\infty}-\frac{\binom{2k}{k}}{2k - 1}x^k\]故
\[g(x) = \sum \limits_{k = 1}^{\infty}\frac{\binom{2k}{k}}{2(2k-1)}x^k = \sum \limits_{k = 0}^{\infty}\frac{\binom{2k + 2}{k + 1}}{2(2k + 1)}x^k\]所以
\[h_k = \frac{\binom{2k + 2}{k + 1}}{2(2k + 1)} = \frac{\binom{2k}{k}}{k+1}\]这样就用生成函数法得到了 $catalan(n)$ 的通项公式。
为什么一开始把 $g(x)$ 平方?
级数乘法规则导致卷积,而 $catalan数$ 的递推式就是卷积的形式,这是 $catalan数$ 的特质。
生成函数法求 $fib$ 数列通项公式
https://oi-wiki.org/math/poly/ogf/#%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97%E7%9A%84%E7%94%9F%E6%88%90%E5%87%BD%E6%95%B0
求 $fib$ 数列通项公式一般用解差分方程的办法就好了,例如链接。这里只是示范生成函数法。
记生成函数 $g(x) = f_0 + f_1x + f_2x^2 + …$ ,这里 $f_i$ 为 $fib$ 数列第 $i$ 项。
$g(x) = f_0 + f_1x + \sum \limits_{n = 2}^{\infty}f_nx^n = f_0 + f_1x + \sum \limits_{n = 2}^{\infty}(f_{n-2} + f_{n-1})x^n = f_0 + f_1x + x^2\sum \limits_{n=0}^{\infty}f_nx^n + x(0 + \sum \limits_{n=1}^{\infty}f_nx^n) = x + x^2g(x) + xg(x)$,所以,
\[g(x) = \frac{x}{1 - x - x^2}\]右边拆有理分式,由于想把其展开为幂级数,所以这里不用 $\frac{A}{x - a} + \frac{B}{x - b}$ 的形式,而是用 $\frac{A}{1 - \alpha x} + \frac{B}{1 - \beta x}$ 的形式,$1 - x - x^2 = (1 - \alpha x)(1 - \beta x)$,$\alpha, \beta$ 为 $x^2 - x - 1 = 0$ 的俩根,解得 $\alpha, \beta = \frac{1 \pm \sqrt{5}}{2}$,待定系数法求出来
\[g(x) = \frac{\frac{1}{\sqrt{5}}}{1 - \alpha x} - \frac{\frac{1}{\sqrt{5}}}{1 - \beta x} = \frac{1}{\sqrt{5}}(\frac{1}{1 - \alpha x} - \frac{1}{1 - \beta x}) = \frac{1}{\sqrt{5}} \sum \limits_{n = 0}^{\infty}(\alpha^n - \beta^n) x^n\]故
\[f_n = \frac{1}{\sqrt{5}}(\alpha^n - \beta^n),其中\ \alpha, \beta = \frac{1 \pm \sqrt{5}}{2}\]总结生成函数法
要求数列 $a_n$ 的通项公式,设生成函数:
\[g(x) = \sum \limits_{n = 0}^{\infty}a_n x^n\]然后另找一条路,利用 $a_n$ 本身的特性(递推公式),将 $g(x)$ 这个幂级数给求出来,然后反过来就知道系数 $a_n$ 的形式了。