cs

二分查找的平均查找长度

二分查找（版本A）

版本A为非searchLast版本，即为：

img

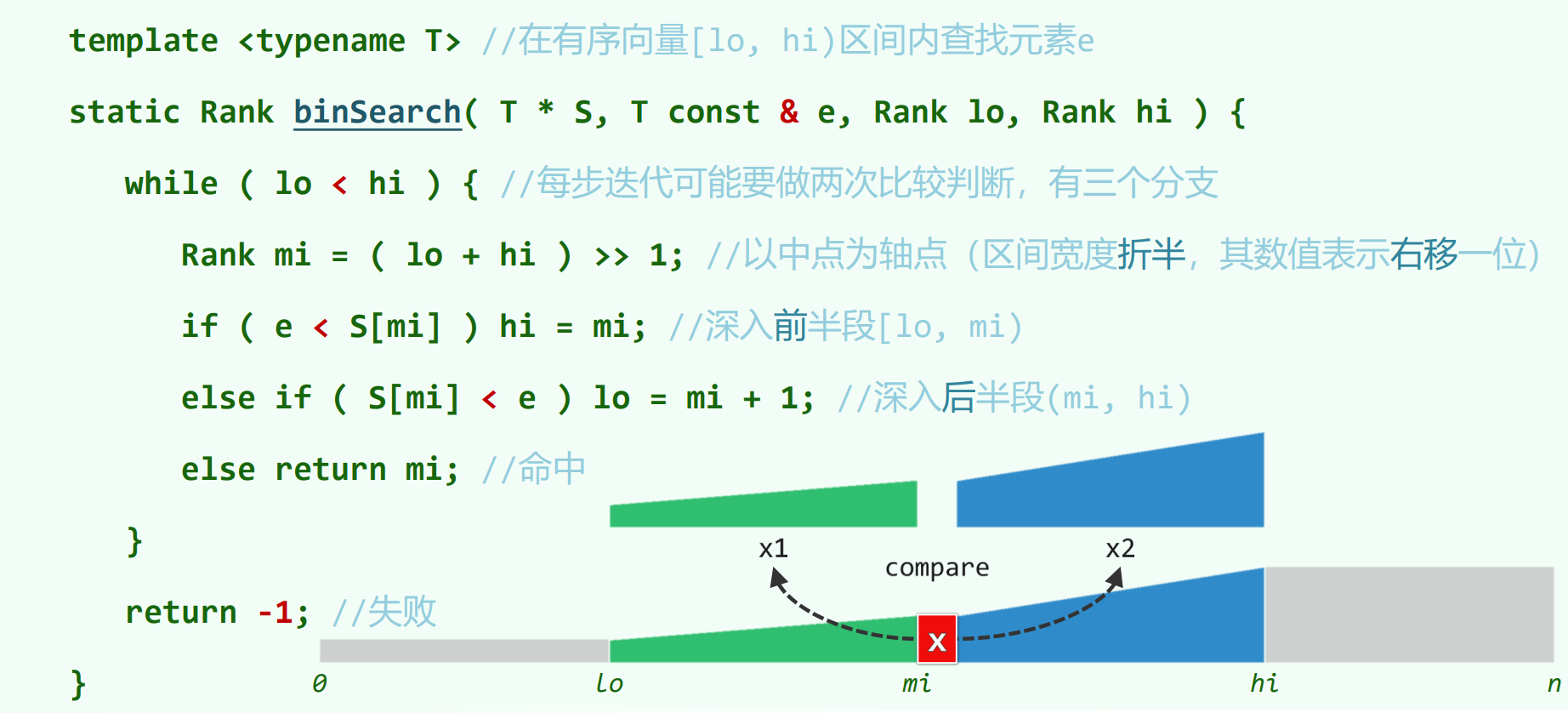
[TODO]: 教材 2.6.5、2.6.6，习题解析[2-20]中有详细归纳分析平均查找长度。

实例计算

img

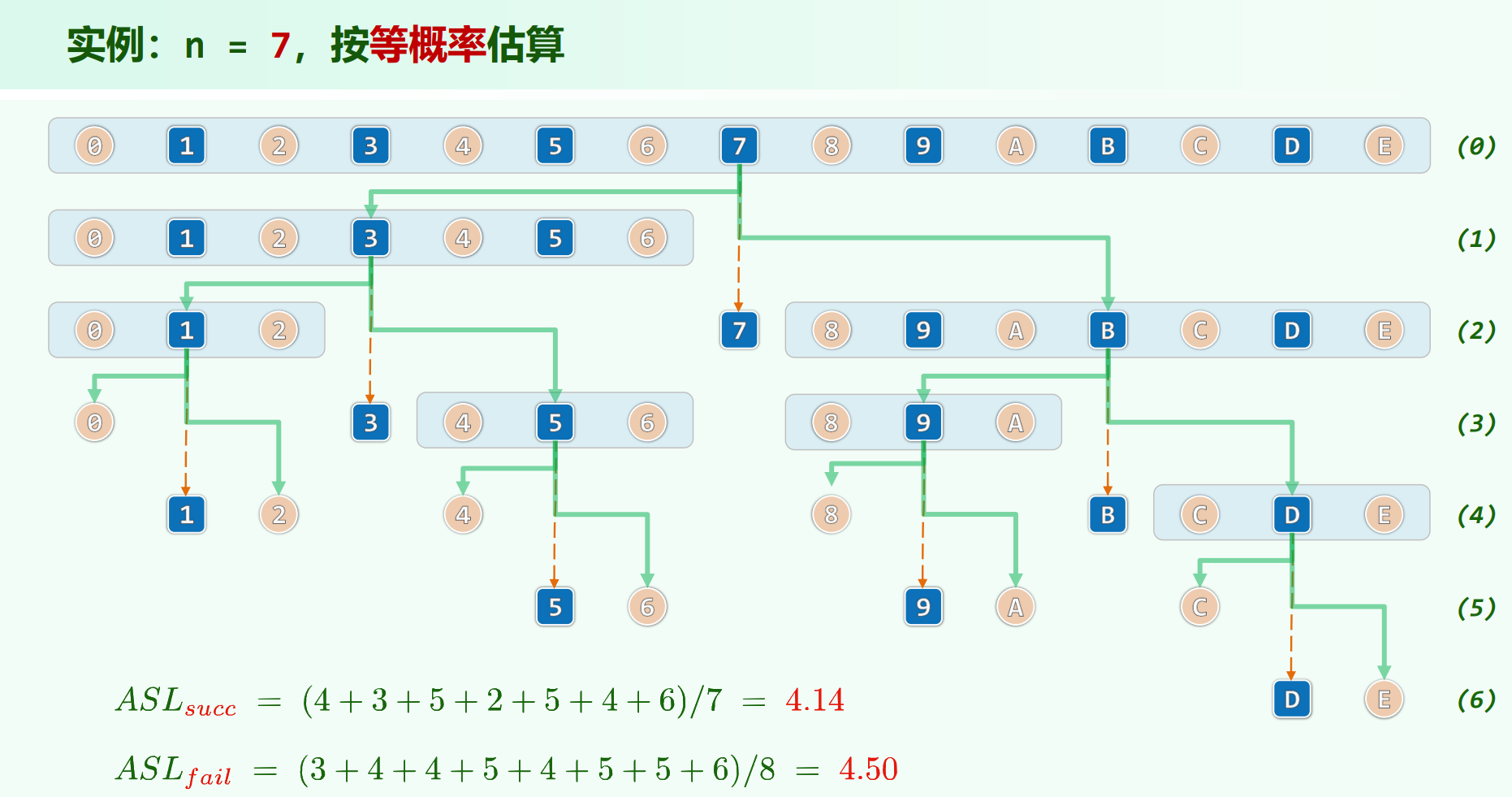
注意，上面的代码是左闭右开区间 $[lo, hi)$，如果向量长度为偶数，$mi = (lo + hi) / 2$ ， $mi$ 会是上中位数位置。

怎么看比较次数？

二分查找里的比较次数（查找长度），看上面的代码。

注意后两种情况都是 $2$ 次。

用图来看：

以上面 n = 7 的查找树为例：

1 是真实的点，走到 1 需要 2 条向左边，1 次定点，查找长度为 $1 + 1 + 2 = 4$ 。

0 是虚拟的点，代表比 1 小，走到 0 需要 3 条向左边，虚拟的点定点不需要开销，查找长度为 $1 + 1 + 1 = 3$ 。

其它点同理。

fib查找

往左需要1次，往右需要2次，让二分不是均匀二分，而是左侧重，往左的概率大，能得到更小的比较次数。

若有 $n = fib(k) - 1$ ，取 $mi = fib(k - 1) - 1$ ，前后子向量长度分别为 $fib(k - 1) - 1 、 fib(k - 2) - 1$ 。

实例计算

计算查找长度的方式与均分的情况相同，只是树是左倾的：

img

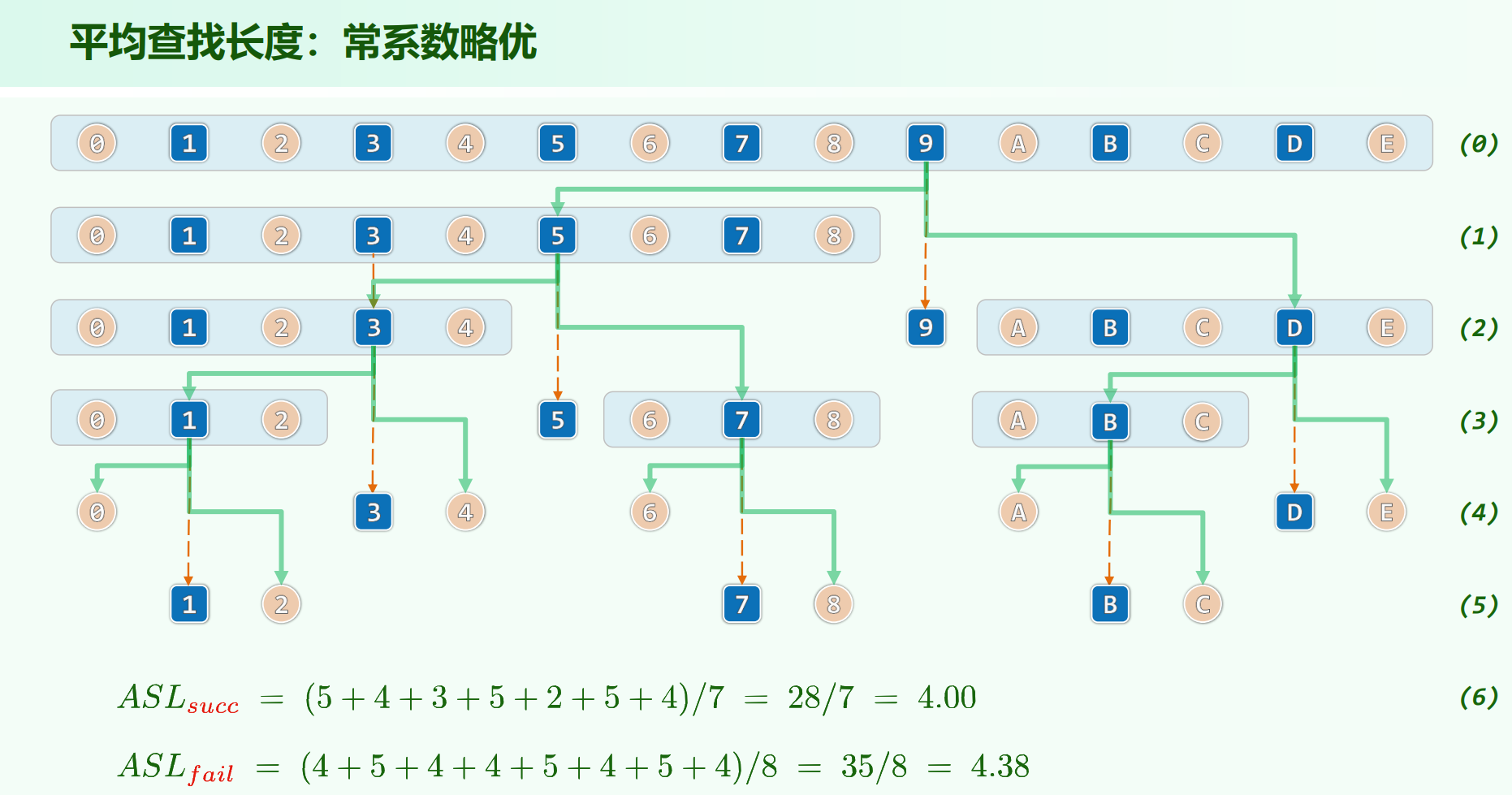
分割点

前后部分应该取何种比例方式分割？

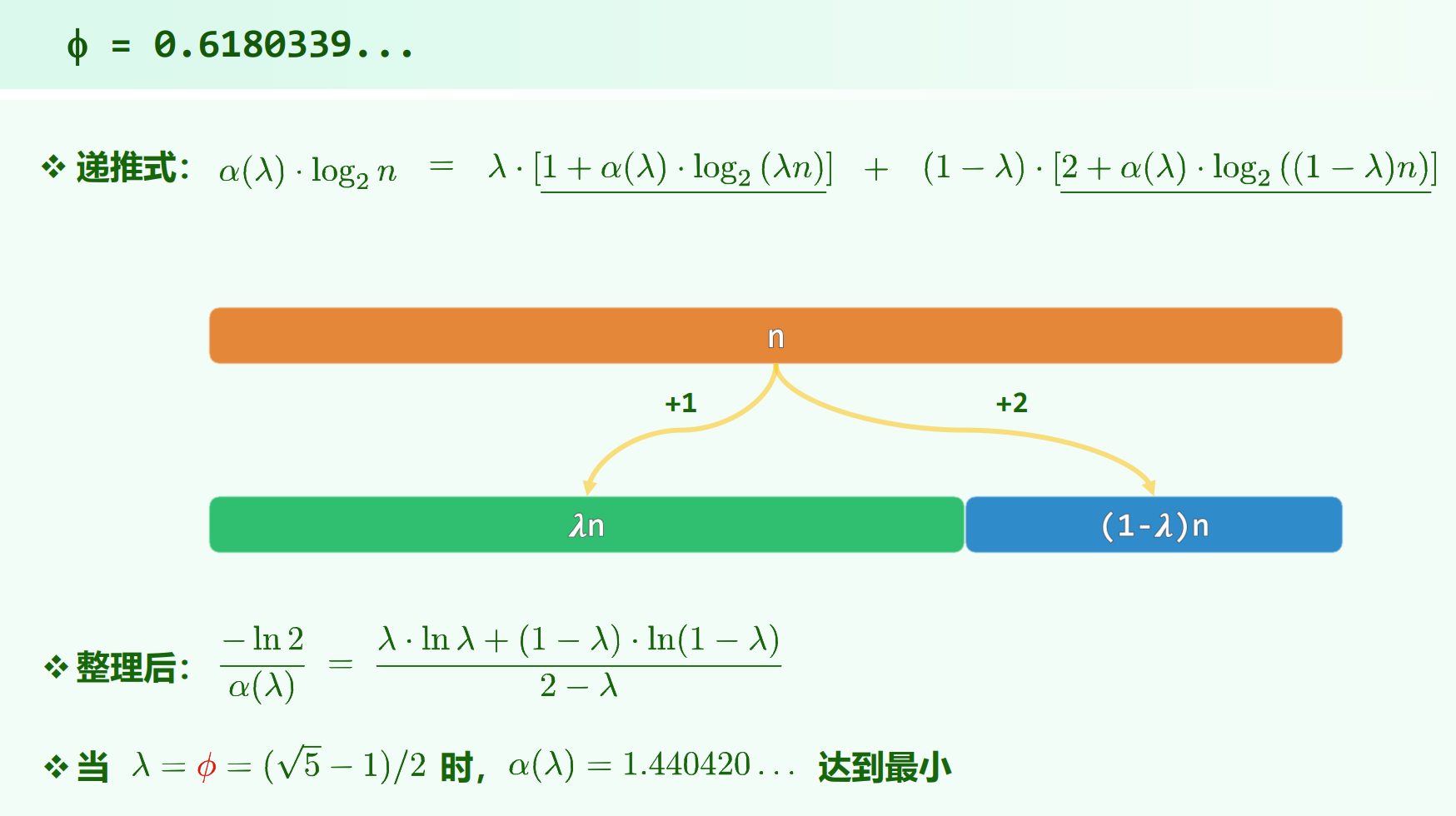
可以不太严谨地假设 $f(n) = \alpha(\lambda)log_2{n}$ ，即 $\lambda$ 的选择影响常系数。

如何让 $\alpha(\lambda)$ 最小？

写递推式，落入左右部分的概率分别为 $\lambda$ 和 $1 - \lambda$ ，于是：

$\alpha(\lambda)log_2{n} = \lambda[1 + \alpha(\lambda)log_2{(\lambda n)}] + (1 - \lambda)[2 + \alpha(\lambda)log_2{((1 - \lambda) n)}]$

整理后得到：

$\frac{-ln2}{\alpha(\lambda)} = \frac{\lambda ln\lambda + (1 - \lambda)ln(1 - \lambda)}{2 - \lambda}$

右边求导之后是：

$\frac{2ln\lambda - ln(1 - \lambda)}{(2 - \lambda)^2}$

(不想手动算的话可以用这个网站)

所以，$\lambda$ 取 $\frac{\sqrt{5} - 1}{2}$ 时，$f(n)$ 最小。

img

img

而对斐波拉契数列，$fib(n) = \frac{1}{\sqrt{5}}[(\frac{1 + \sqrt{5}}{2})^n - (\frac{1 - \sqrt{5}}{2})^n]$

后项/前项的极限为黄金分割比 $\frac{1 + \sqrt{5}}{2}$ ，而上面 $\frac{\lambda}{1 - \lambda} = \frac{\frac{\sqrt{5} - 1}{2}}{1 - \frac{\sqrt{5} - 1}{2}} = \frac{\sqrt{5} + 1}{2}$ 也是黄金分割比。所以fib查找的分割方式是最优的。

这个方法，有点神奇，写了下递推式，就无中生有可以做了。

二分查找（版本B/C）

即为常见的searchLast/searchFirst的写法。

只有两种分支情况，往左/往右走都只需 $1$ 次比较，相当于以 $+1$ 的开销进入左子向量/右子向量。

平均查找长度(Average Search Length)结论

二分查找版本A:

$ASL_{succ} = O(1.50 \cdot logn)$

$ASL_{fail} = O(1.50 \cdot logn)$

fib查找：

$ASL_{succ} = O(1.44 \cdot logn)$

$ASL_{fail} = O(1.38 \cdot logn)$

二分查找版本B/C:

$ASL_{succ} = O(1.00 \cdot logn)$

$ASL_{fail} = O(1.00 \cdot logn)$