cs
- 08.Advanved Search Trees.pdf P80
动机
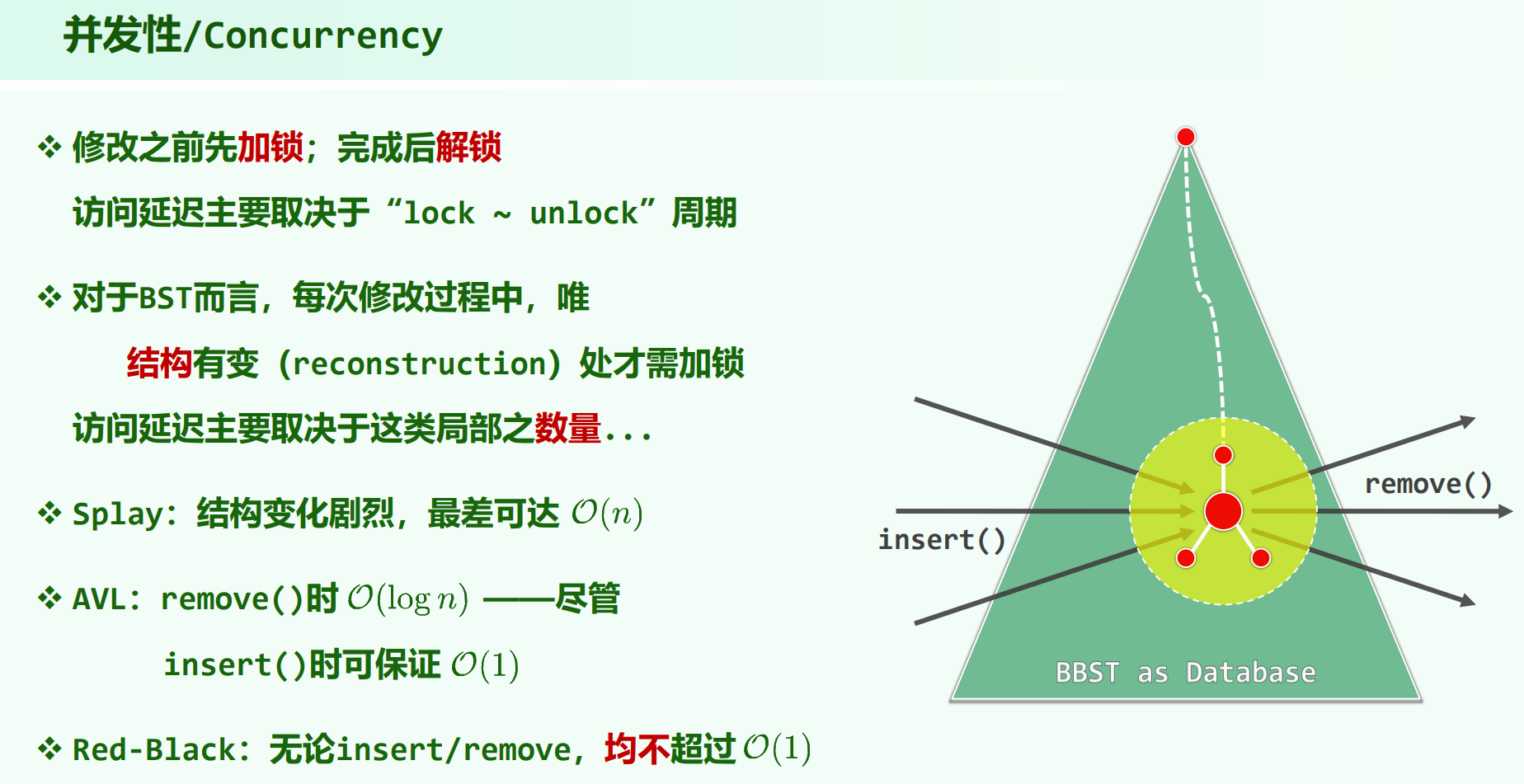
注意以上是在说拓扑结构的变化量,不是时间复杂度。
红黑树的 insert / remove,拓扑结构变化只会有 $O(1)$ 次,但是颜色变化可达 $O(n)$ 次。
定义
-
树根必为黑色
-
外部节点视为黑色
-
红节点的孩子和父亲都必须是黑色
只需保证红节点的孩子是黑色,就可以保证红节点的父亲是黑色了
-
从根到任意外部节点的路径,经过的黑节点数目都必须相同
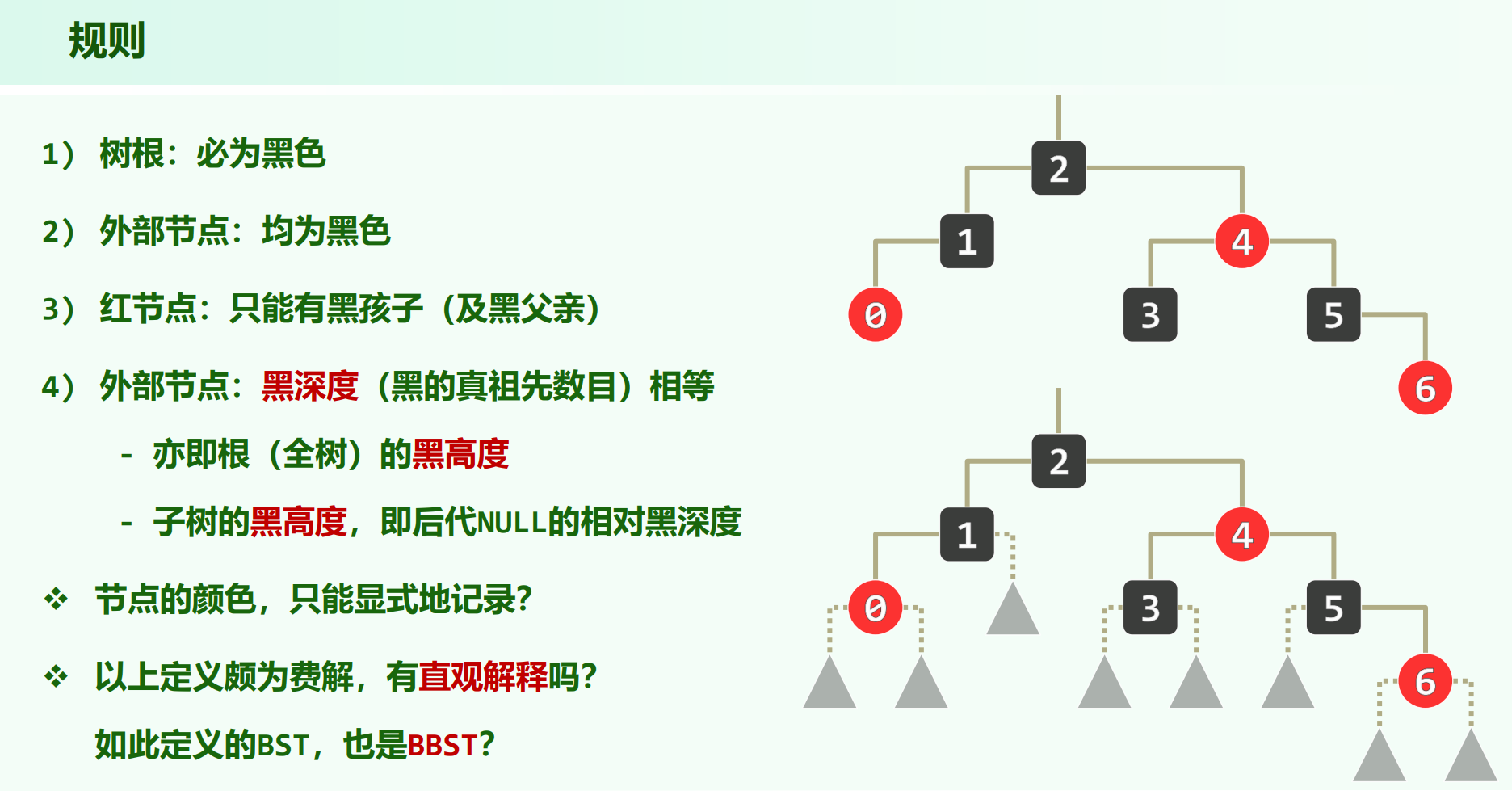
-
黑深度:往上走到根(不包括自己)的黑节点数目。
(书上黑深度的定义与ppt上有些许不同,这里的是ppt上的定义)
-
黑高度:从子树根往下走到外部节点(包括子树根,不计数外部节点)的黑节点数目。
(也就是说黑高度实际没把外部节点当作真实存在,没计数它,本来外部节点也只是nullptr)
全树的黑高度为根节点的黑高度,也就是说全树的黑高度是计数任意一条路径上的黑节点数,但不包括外部节点。
注意以上定义实际是在数黑节点数,和边无关。
红黑树 与 (2,4)-树 的对应关系
每个黑节点的左右孩子若为红(反过来,红节点的父亲一定存在且为黑),则将其收到黑节点中,这样,红黑树表面上不会有红节点,每个节点中都恰有一个黑节点作为核心,可能有红节点作为陪衬。由于黑高度都相等,所以叶子节点也都在同一层。
也就是说,红黑树可以变换为$4$阶B树,对于$4$阶B树,也可以视节点内的关键码数将关键码染红下放,变换为红黑树。
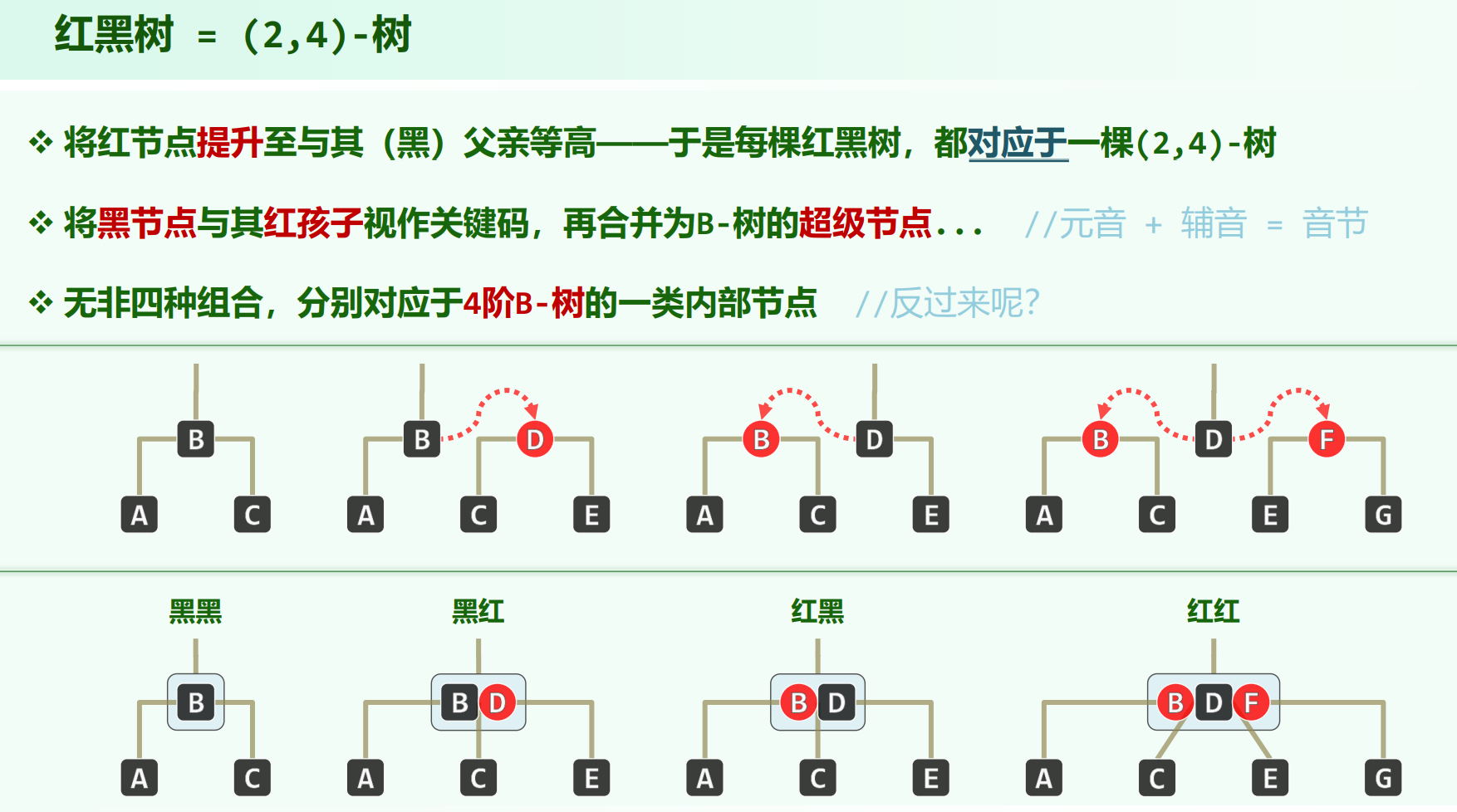
注意,在B树节点里谁红谁黑是确定的,谁是父节点谁黑,其它为红,有3个关键码的话一定是中间那个黑。
红黑树的高度
记包含 $n$ 个内部节点的红黑树的高度为 $h$ ,则有:
\[log_2(n + 1) \le h \le 2 \cdot log_2(n + 1)\]红黑树的高度也是 $O(logn)$
左边的 $log_2(n + 1)$ 显然,是按最平衡的二叉搜索树来算的,不可能比这低。不过由于红黑树的高度要算外部节点,所以n = 1时高度为1,n = 3时高度为2,n = 2^k - 1时高度为k,所以高度是 $\lceil log_2(n + 1) \rceil$ ,如果是完全二叉树的话高度该是 $\lceil log_2(n + 1) \rceil - 1 = \lfloor log_{2}n \rfloor$。
右边的 $2 \cdot log_2(n + 1)$ :
红黑树的高度要算外部节点,所以树高 = 最多红节点的路径上的黑红节点数相加。
考虑红黑树的红高度 $R$ 与黑高度 $B$ ,红节点最多与黑节点一样多(黑红黑红…),所以 $R \le B$ ,$h = R + B \le 2 \cdot B $ 。把红节点都收到黑节点里,红黑树的黑高度转化成了对于4阶B树的高度,于是:
\[h \le 2 \cdot B = 2 \cdot (1 + log_2\frac{n + 1}{2}) = 2 \cdot log_2(n + 1)\]插入
插入的节点都是以红色插入
插入的节点 $x$ 若为根,说明红黑树为空,直接把根 $x$ 染成黑色即可(实际教材P231代码并不需要单独处理这种情况,节点插入之后solveDoubleRed(x),如果x是根的话直接染黑并height++即完毕)
否则:
插入的 $x$ 为红色,其父亲必存在,
-
若为黑,则插入完毕
-
若为红,要进行双红修正
双红修正看 (插入点)$x$ 的 $uncle$ 颜色,牵涉到的节点为插入节点 $x$,以及 $x$ 上区域的三个节点 $p, g, u$ 。
双红修正:
$RR-1$:$u$ 为黑


如果是刚插入那次的话 $u$ 是外部节点,但是 $u$ 也可能不是外部节点,因为 $RR-2$ 可能向上传播出现双红,向上传播之后如果双红是 $RR-1$ 的情况的话 $u$ 就不是外部节点。
用等价的B树来看,$RR-1$ 相当于B树节点里有 $3$ 个关键码,但是黑的不在正中间。那么将中间的节点变成黑色,旁边两个变成红色,再连回红黑树子树原本的父节点就行了。
这等价于 ${x, p, g}$ 去做 1次connect34 + 2次染色($g$一定由黑边红,因为其一定当不了 $b$ ,然后当 $b$ 的那个节点由红变黑)。
由于 $RR-1$ 四棵子树的根节点一定都为黑($u$ 为黑是因为这里是我们的讨论情况),调整后的子树根为黑,子树黑高度也不变,$a$ 和 $c$ 也不会构成新的双红。调整随即完成。
$RR-2$:$u$ 为红
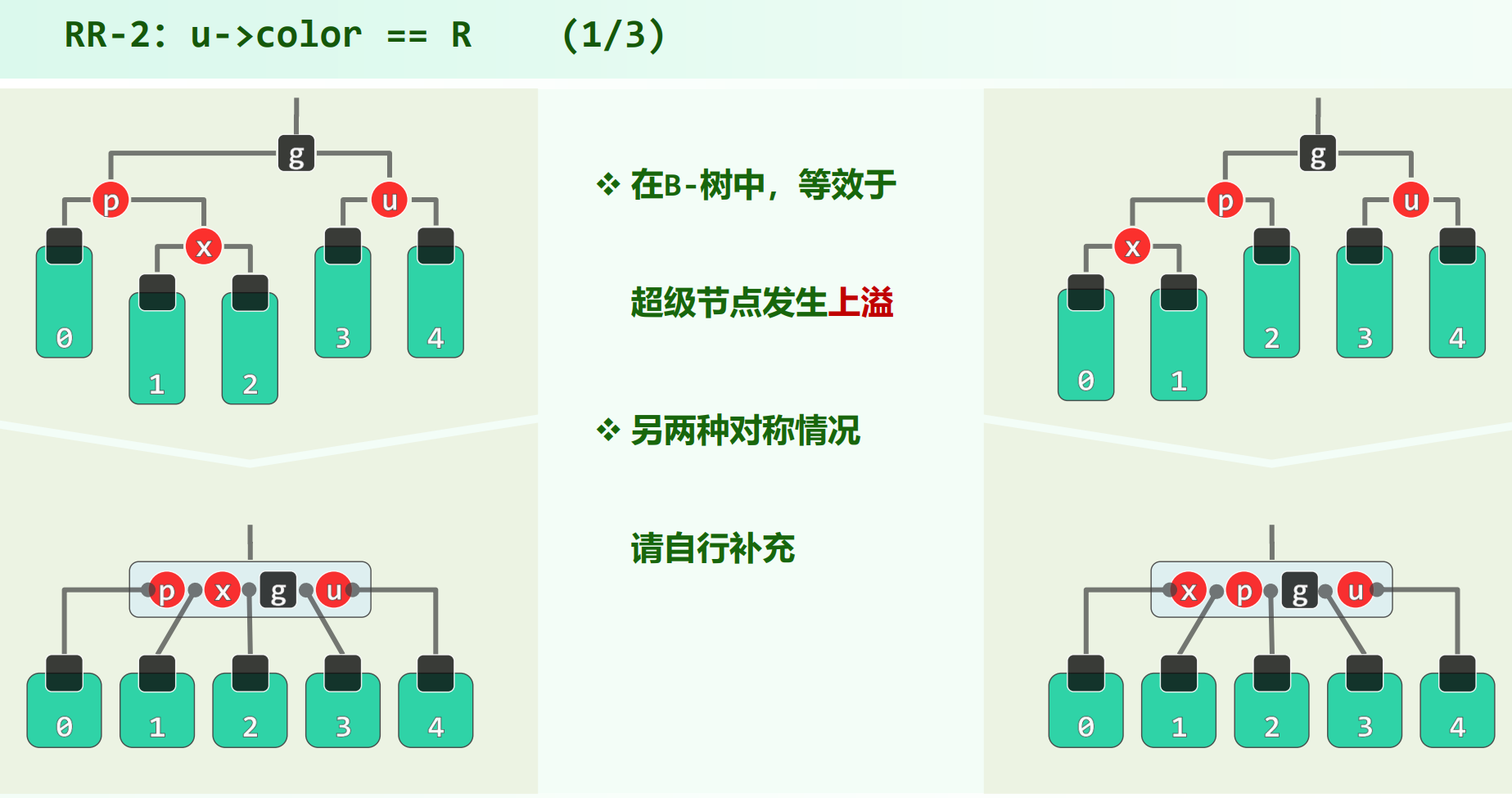
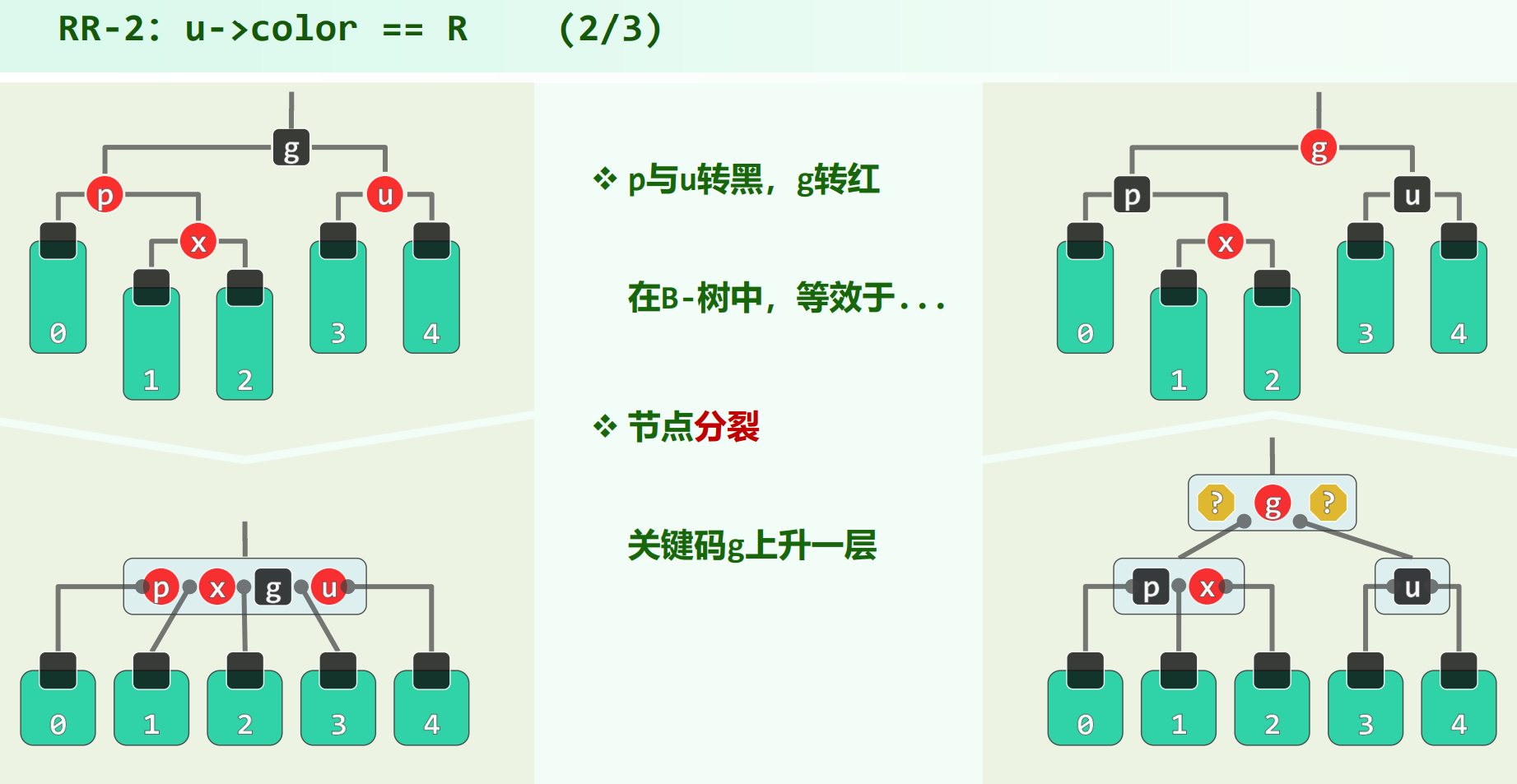
转成对应B树,把红后代收进黑节点,可以看到是关键码太多,节点上溢了。因此,把 $g$ 升上去,注意 $g$ 升上去,子节点 ${p, x} \ {u}$ 中的核心必须染黑,为了维持黑高度不变,这说明升上去的节点 $g$ 要染红,下面的两个节点中的关键码谁染黑也是确定的,谁是父亲谁是核心,谁是核心谁染黑,所以一定是 $p$ 和 $u$ 变黑。
注意这里红黑树与B树的对应关系的微妙差别,B树代码里是固定选下标为 $s = \lfloor \frac{m}{2} \rfloor$ 处的关键码。但是上图的对称情况,如 $\textcolor{red}{u} {g} \textcolor{red}{p} \textcolor{red}{x}$ ,由于 $g$ 原本就是红黑树中最祖先的那个节点,所以在B树中不能是选中间偏右的 $p$ 上去,不然在对应的红黑树中要调树结构,还是要选 $g$ 上去。
$RR-2$ 其实就是 $g$(黑) 与 $g$的儿子层(2红) 颜色互换一下。只需 $3$ 次染色,不会调整结构。
$RR-2$ 调整之后,子树性质满足,黑高度不变,但是由于子树根 $g$ 变红了,双红可能向上传播(正如同B树分裂会向上传播)。传播从 $x$ 到 $g$ 上升两层。新出现的双红可能是 $RR-1$,也可能是 $RR-2$,递归判断处理。若处理传播到了根(一次$RR-2$处理完后发现 $g$ 为根),则直接将根染黑即可处理完毕,红黑树的黑高度增加 $1$ 。
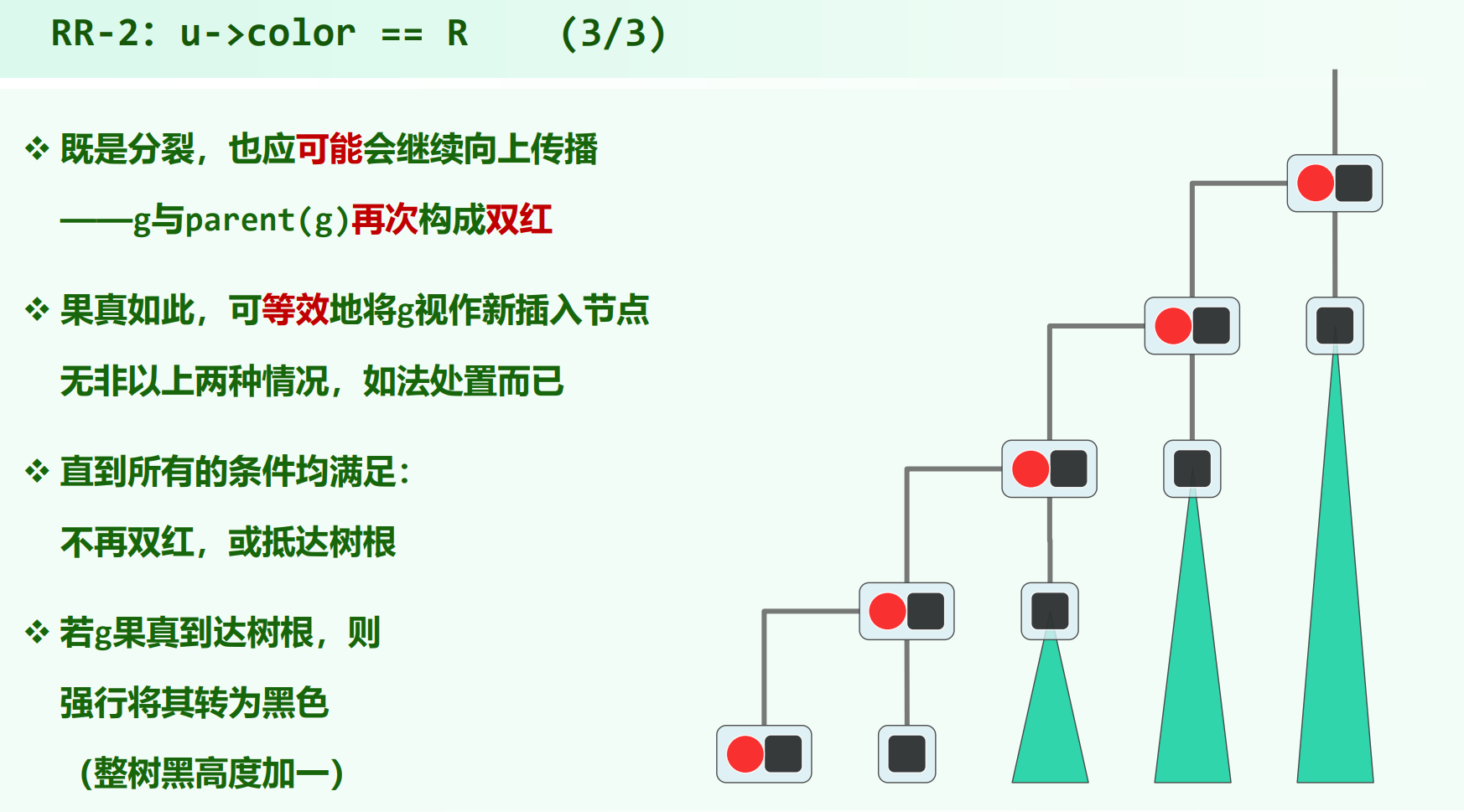
双红修正总结
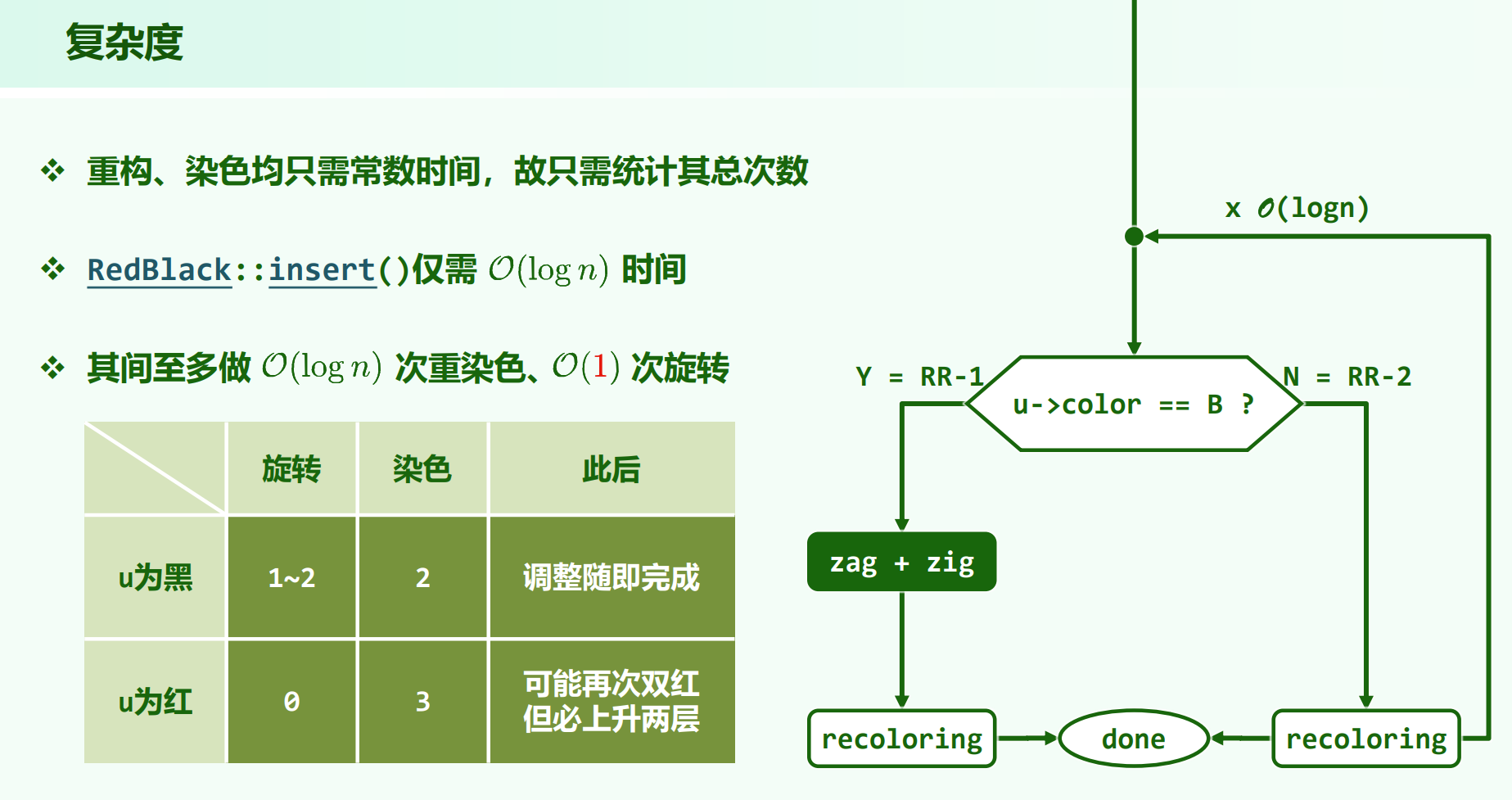
-
$u$ 为黑 $\Rightarrow$ $RR-1$ ,${x, p, g}$ 去做 1次connect34 + 2次染色。调整完毕。
-
$u$ 为红 $\Rightarrow$ $RR-2$ ,交换 $g$(黑) 与 $g$的儿子层(2红) 颜色。可能再次双红,但必上升两层到 $g$ 。
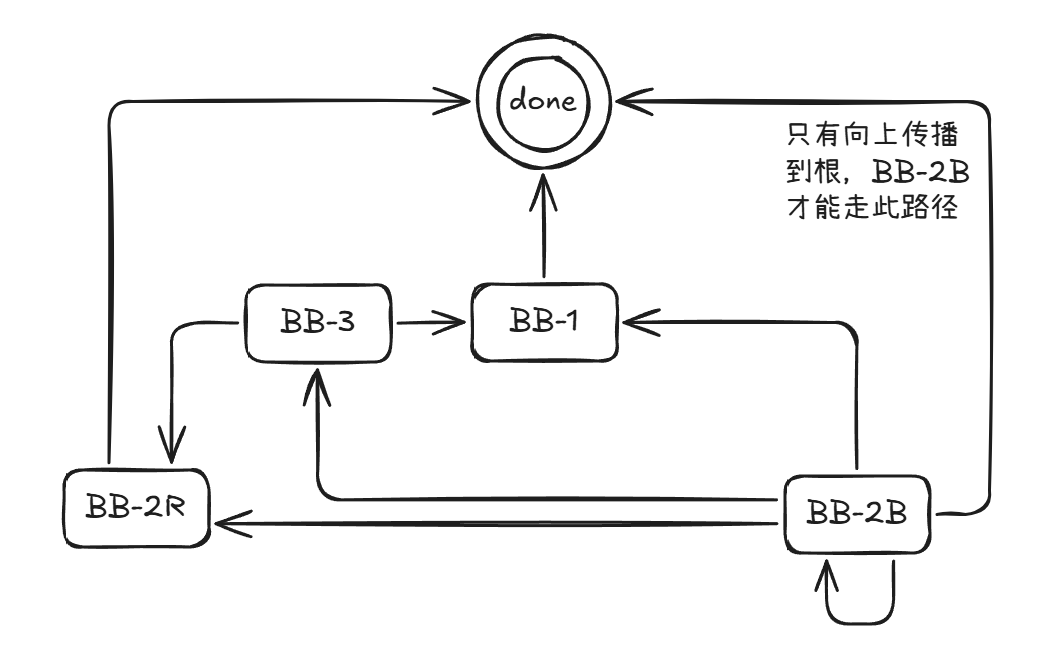
双红修正状态机
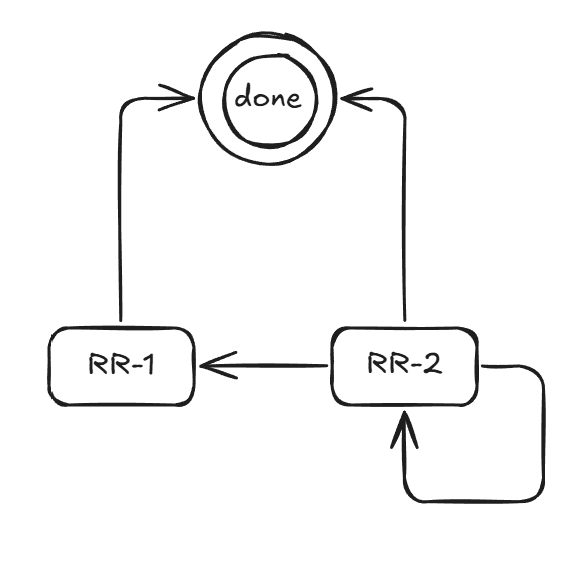
删除
删除比插入要复杂很多,B树也是这样。
首先,删除要先按BST的删除步骤,把要删除的关键码换到单分支节点上,以下直接从完成了这步开始讨论。
以下出现的x表示要删除的位置,r表示要删除位置的儿子(可能为外部节点nullptr),x/r表示r已经接替了x的原位置。
如果x和r其一为红,则另外一个一定为黑,二者一黑一红,只要把接替者r染成黑的,黑高度就会不变,删除操作随即完成:
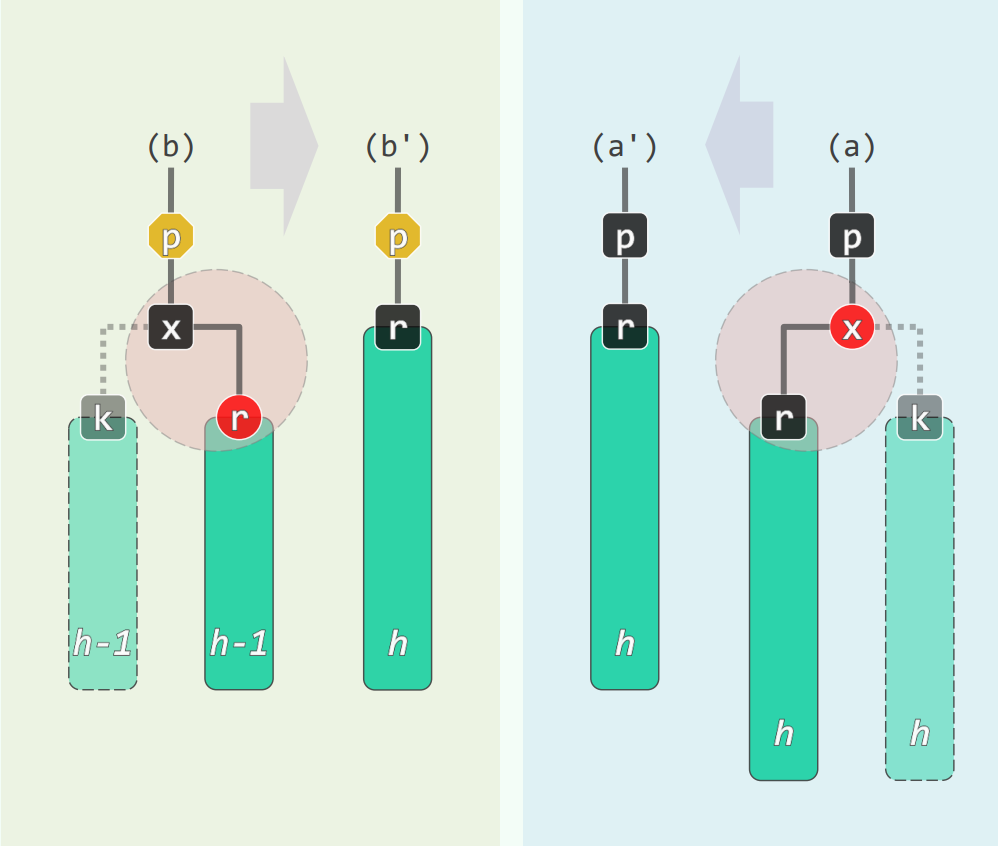
如果x和r都为黑,则删除x会导致x/r处的黑高度少了 $1$,需要进行双黑修正。
solveDoubleBlack(Node* r)(教材P238)的含义是,r是当前的处理位置,由于双黑的删除,导致子树r的黑高度缺了 $1$ ,要通过双黑修正处理这个问题。
以下邓老师ppt中都是先把x和r写上了,没有上来就是x/r,这一部分原因是为了更好地看清另一侧的黑高度,比如BB-2R,由于删除之前左边黑高度至少为2,所以s一定不是外部节点nullptr,给s染红不会有问题。此外,代码上会有一个问题,由于r可能是外部节点nullptr,所以如果一开始就把节点x删了,通过r可能无法找parent,这个的解决办法之一是调整完后再把x删掉。之所以提这个问题是因为,用可视化网站去试BB-3,如果r是nullptr,并立刻删除x,以r接替,一单旋容易找不到原本的处理位置r在哪里了,因为分辨不清是哪个nullptr。BB-1、BB-2R、BB-2B 都没有这个问题,前两者调一次之后就完毕了,BB-2B是因为调整之后处理位置会上升一层到p认得出来。只有BB-3有这个问题,不过手工做的话应该还好,给那个nullptr标记一下。
双黑修正先明确处理位置r,牵涉到的节点为处理位置r,以及 r 左区域的兄侄父stp (1 + 2 + 1)个节点,要先后看 s, t, p 是否为红色。
s(sibling,也是 r 的 uncle) 为红,落到 $BB-3$
t有红,落到 $BB-1$
p为红,落到 $BB-2R$
落到$BB-2B$
确定了要做哪种双黑调整操作后就简单了。
双黑,删除x,相当于对应B树中x所在节点下溢,接下来即为双黑修正去处理子树x/r缺少的 $1$ 黑高度:
s为黑,s有红孩子t —— $BB-1$
如果s有两个红孩子,选哪个为t都可以,这里不像AVL树那样如果不优先选成同侧可能导致错误。
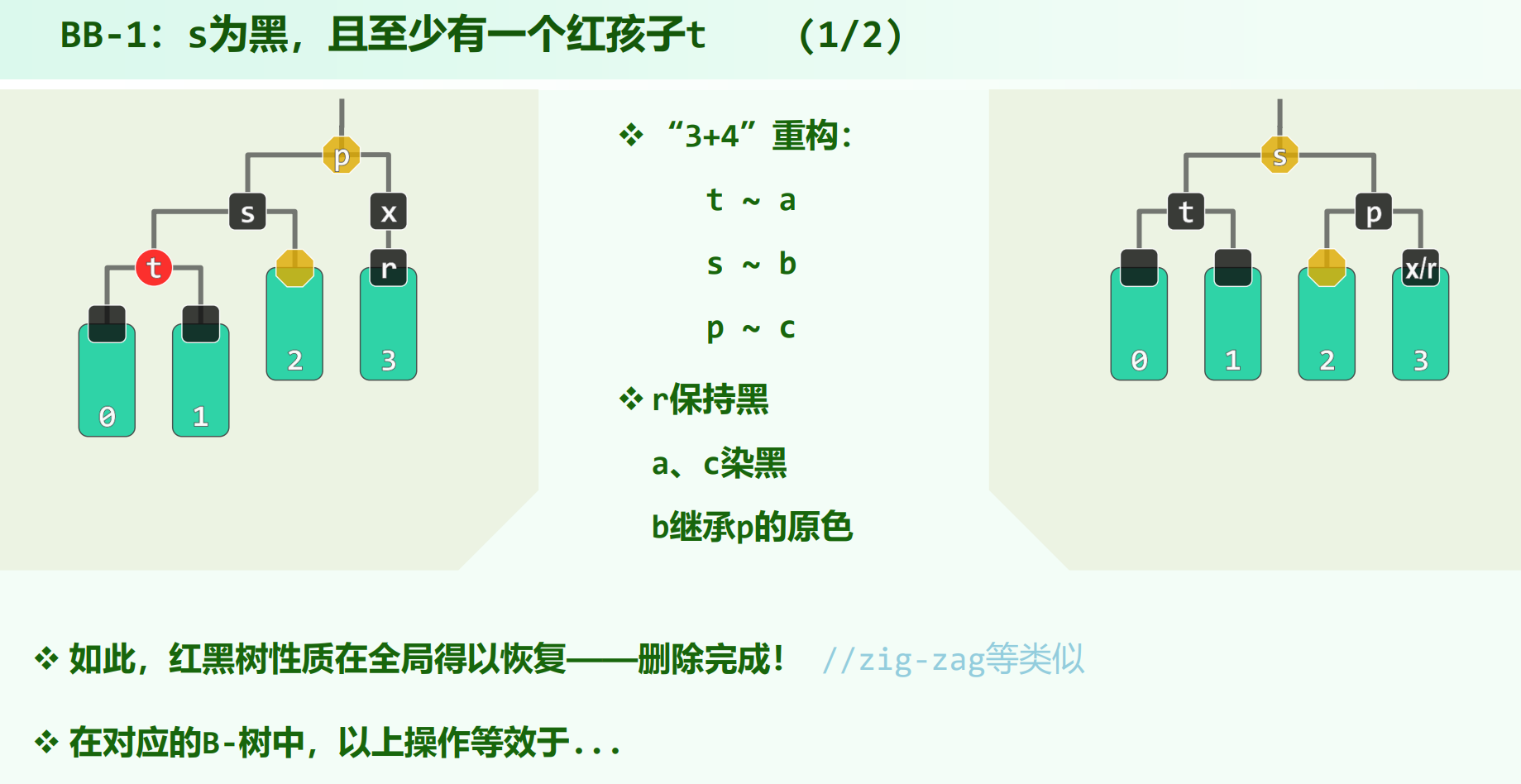
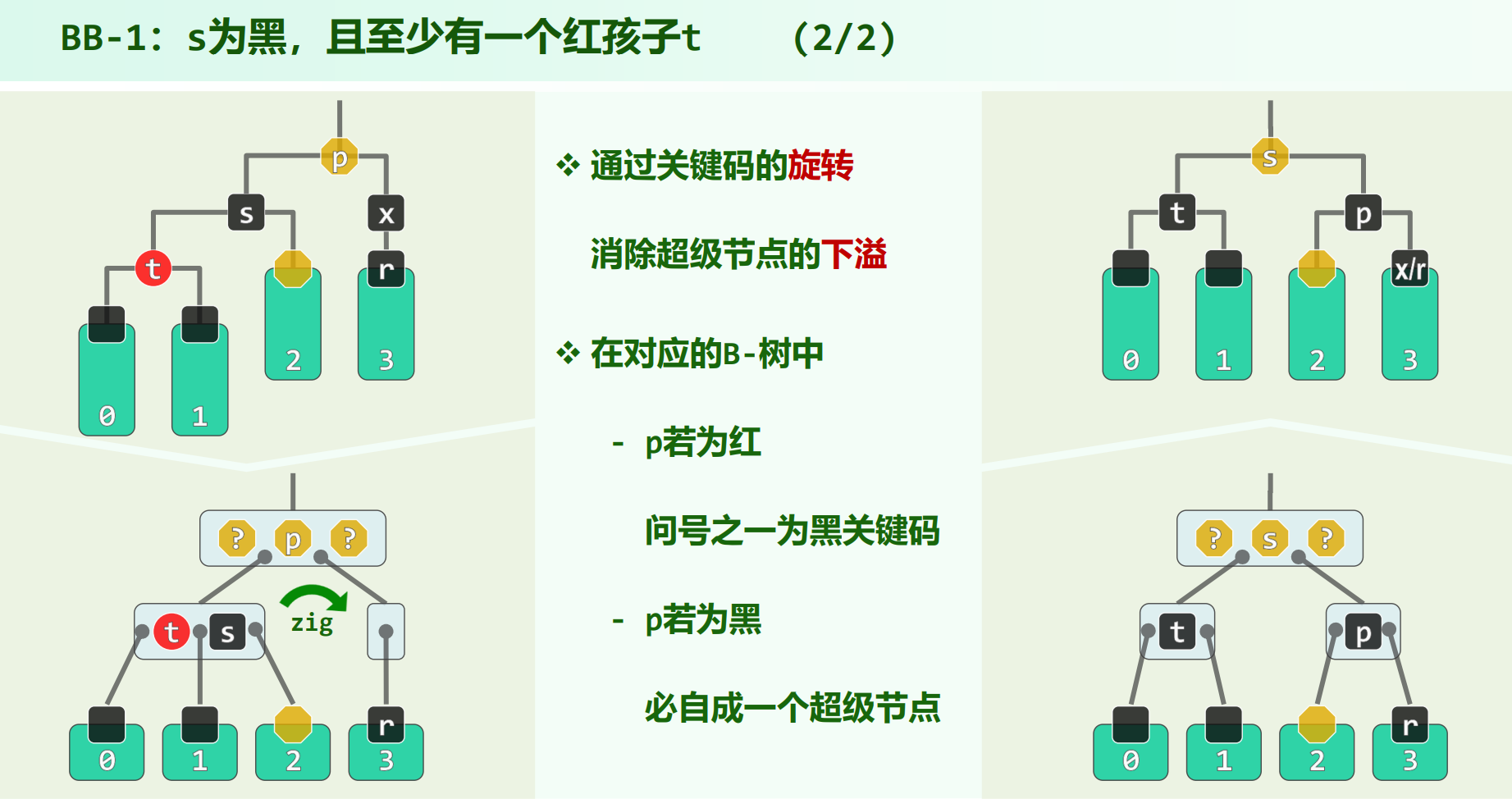
这种情况相当于B树下溢后兄弟够借的情况,${p, s, t}$ 去做 1次connect34 + 3次染色,b去继承子树根p的原颜色,a、c都染成黑色。调整随即完成。
这里与 $RR-1$ 不同,虽然也是 connect34 ,但是要染 $3$ 次色,有可能出现例如p原本就是黑色,现在也染成黑色的情况,但是加个判断不如直接就赋值。
s为黑,s无红孩子,p为红 —— $BB-2R$

这种情况相当于B树下溢后兄弟不够借,从父亲那里借个节点粘接,借下来的节点为红(父节点一定不会下溢)。
问题来了:s黑 和 p红 粘在一起,就这样就好了吗?
要交换下二者颜色。把降下来的节点p染黑,于是s就变红(这里和 $RR-2$ 升上去的 $g$ 变红是一致的升红降黑原则)。如果选择s黑p红,那么s应当是p的父亲,还要去调结构。
$BB-2R$ 其实就是把 s 和 p 的颜色互换一下,变成s红p黑。调整随即完成。
由于此情况s无红孩子,所以s变红不会导致双红。
s为黑,s无红孩子,p为黑 —— $BB-2B$

这种情况相当于B树下溢后兄弟不够借,从父亲那里借个节点粘接,借下来的节点为黑(由于s为黑,父节点里没有其它关键码,一定下溢)。
p移下来后和 $BB-2R$ 的下移原则一样,其该为黑色(p原本也是黑色),s要变红。
$BB-2B$ 其实就是把s变红。但必将再次双黑,但将上升一层(这里说的必将再次双黑并不是说p的parent一定为黑,而是子树p的黑高度缺了 $1$ ,就好像p接替了一个被删的黑节点一样。)。这种情况双黑会向上传播,如果传播到根,整树的黑高度降低 $1$ 。
只能是 $BB-2B$ 使红黑树的黑高度变低,且由于只有 $BB-2B$ 能进 $BB-2B$ ,整树黑高度降低 $1$ 的情况一定是一路 $BB-2B$ 到根。
$BB-2B$ 其实是:$p, s, t$ 全是黑的,根本没有红节点可供操作以弥补缺 $1$ 的黑高度,所以只能尽力而为,把s变黑,让p的左右子树黑高度相等,p的黑高度则缺了 $1$ ,然后下一步solveDoubleBlack(p)。
s为红 —— $BB-3$

这种情况相当于B树下溢后兄弟不够借,从父亲那里借个节点粘接,借下来的节点为黑(由于s为红,父节点里还有个s,一定不会下溢)。但是这里和 $BB-2B$ 里的升红降黑原则不一样了,降下来的节点p是要染红的,父节点里剩下的s染黑。
$BB-3$ 等价于 $s, p$ 在 $p$ 处单旋,并如同 $BB-2R$ 一样交换s, p颜色。这种情况要调整的位置仍在x处,但是情况变成了 $BB-1$ 或 $BB-2R$ 。
双黑修正总结
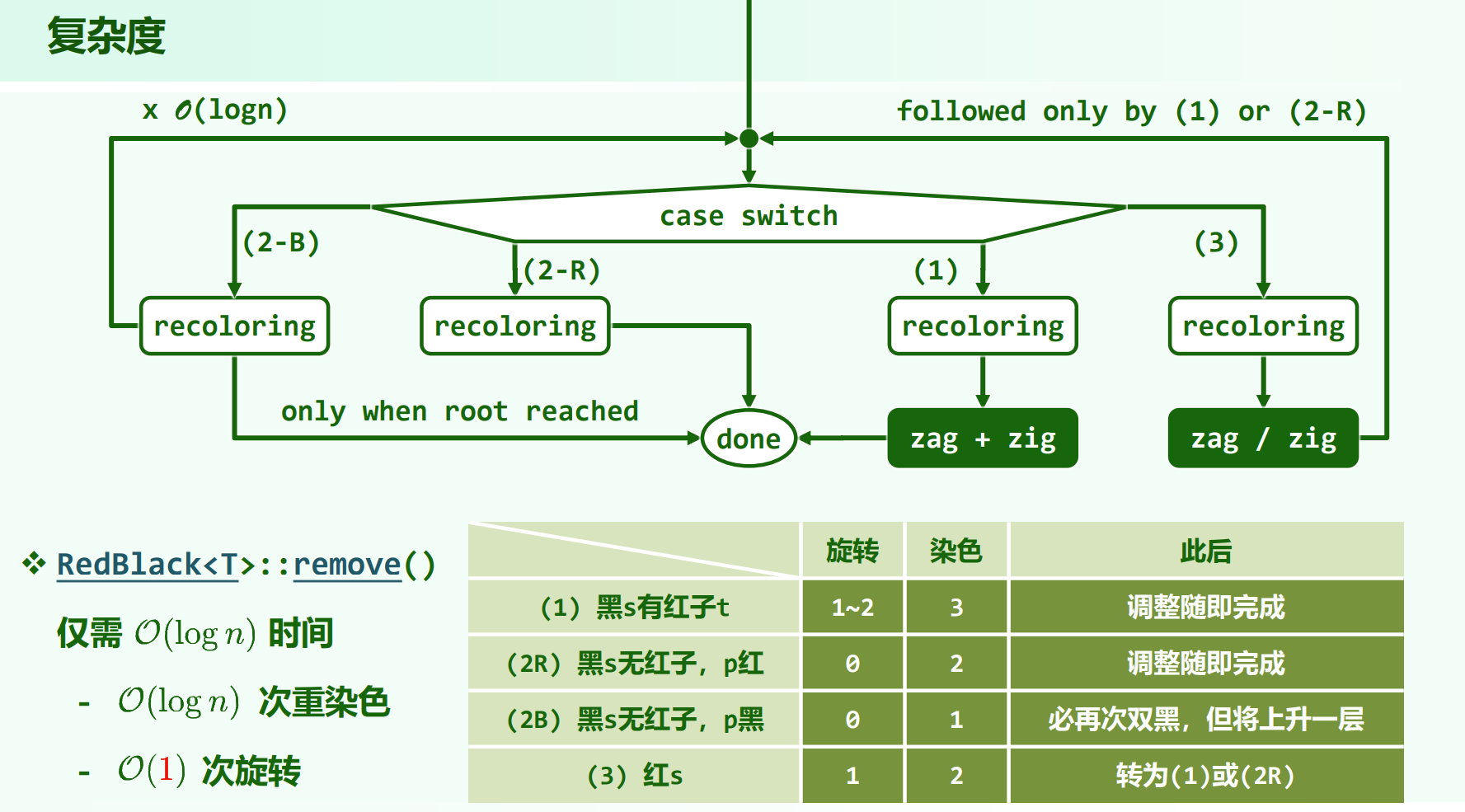
只要 ${p, s, t}$ 有红的,都可以操作修复黑高度,不会发生向上传播的情况。
-
$s$ 红 $\Rightarrow$ $BB-3$ ,$p$ 处单旋,交换 $s$, $p$ 颜色,一定会转为 $BB-1$ 或 $BB-2R$ 。
-
$s$ 黑
-
$s$ 有红孩子 $\Rightarrow$ $BB-1$ ,${p, s, t}$ 去做 1次connect34 + 3次染色,
b去继承子树根 $p$ 的原颜色,a、c都染成黑色。调整完毕。 -
$s$ 无红孩子
-
$p$ 为红 $\Rightarrow$ $BB-2R$ ,交换 $s$, $p$ 颜色。调整完毕。
-
$p$ 为黑 $\Rightarrow$ $BB-2B$ ,把 $s$ 变红。一定继续双黑,上升一层到 $p$ 。
-
-
双黑修正状态机