cs
- 08.Advanved Search Trees.pdf P1
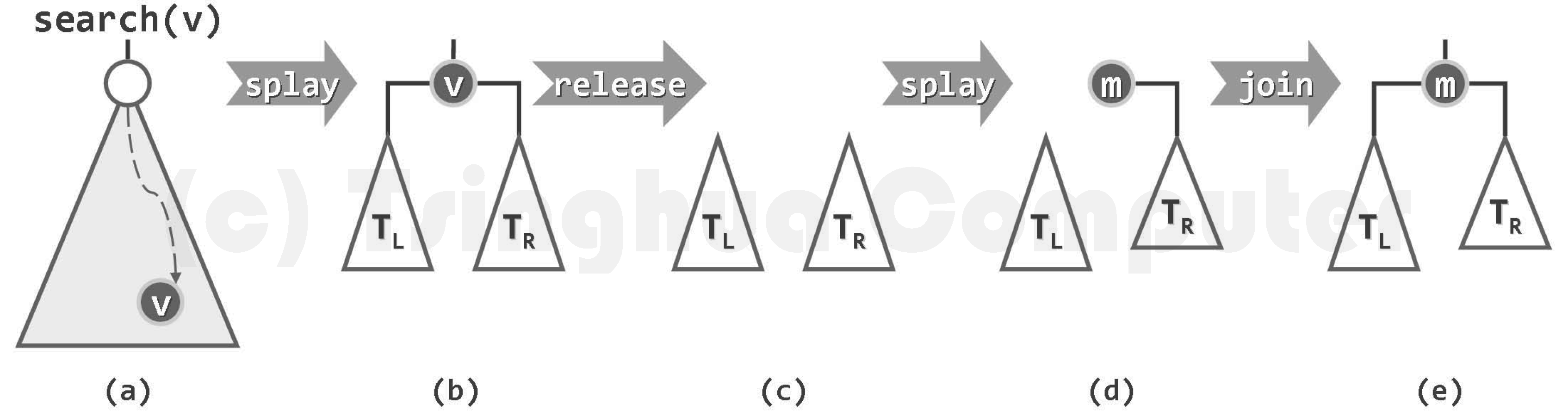
伸展树
将刚被访问的节点,转移至根。
这里不像AVL树一样有失衡的概念,不是从失衡节点 $g$ 找 $p$, $v$ 。而是刚被访问过的节点为 $v$ ,父和祖父为 $p$ 和 $g$ 。
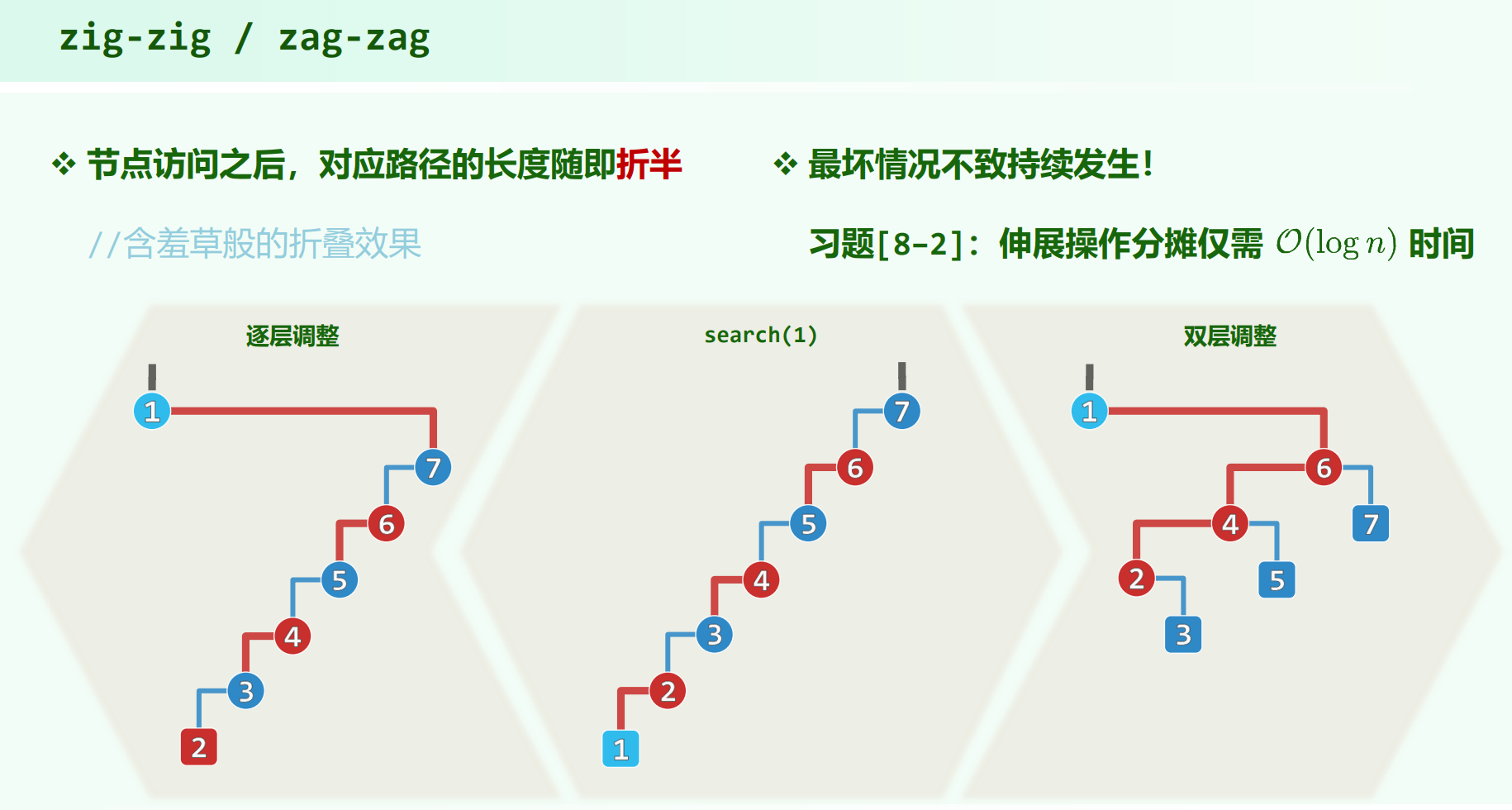
逐层伸展
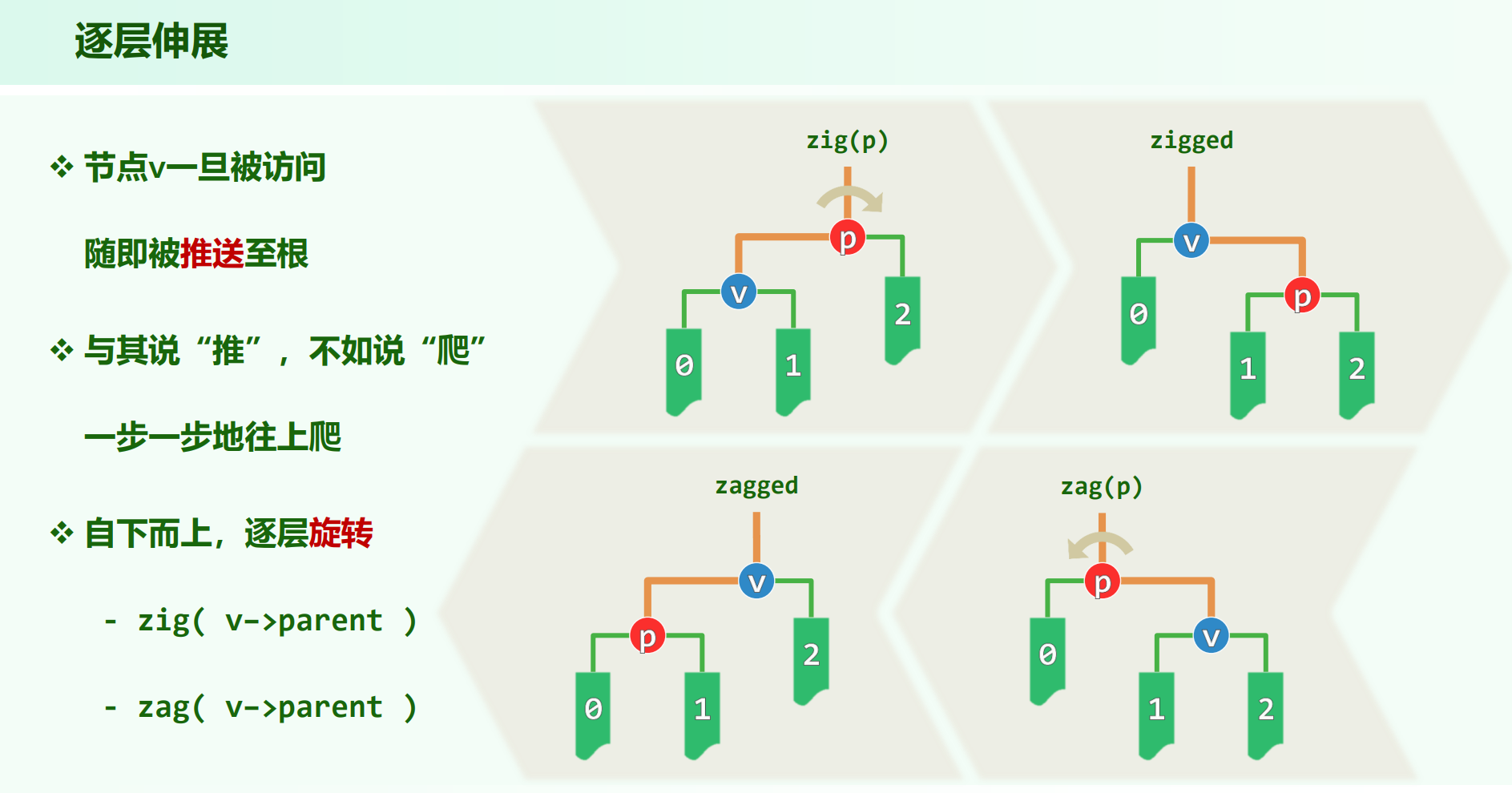
通过单层伸展把 $v$ 转上去。
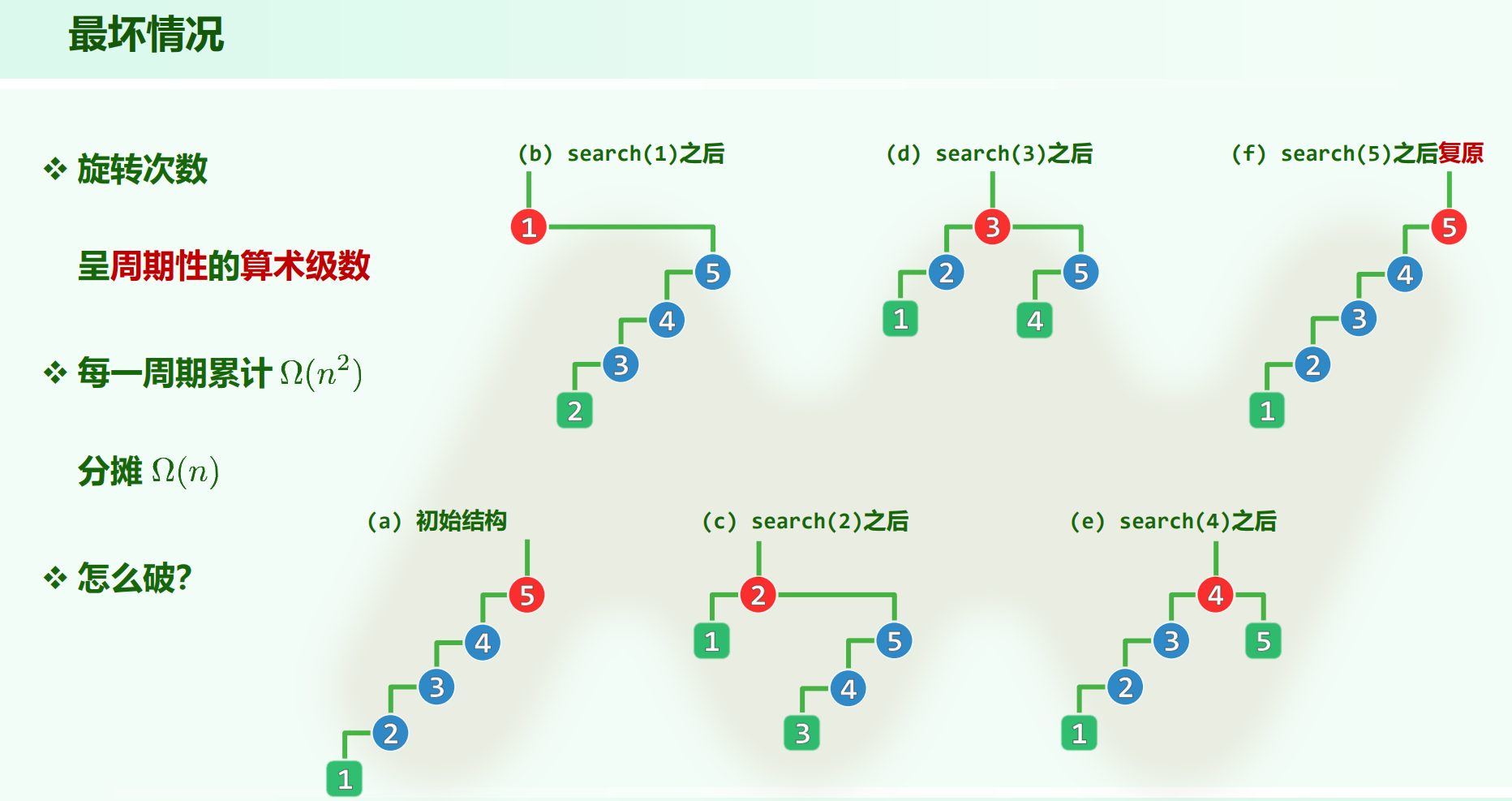
逐层伸展的问题
对于伸展树,按单调顺序插入节点,一定会得到一个单链。然后再按单调顺序访问一遍,可以看到,每次树高只减了 $1$ ,整个过程开销为 $O(n^2)$ ,分摊时间复杂度 $O(n)$
双层伸展
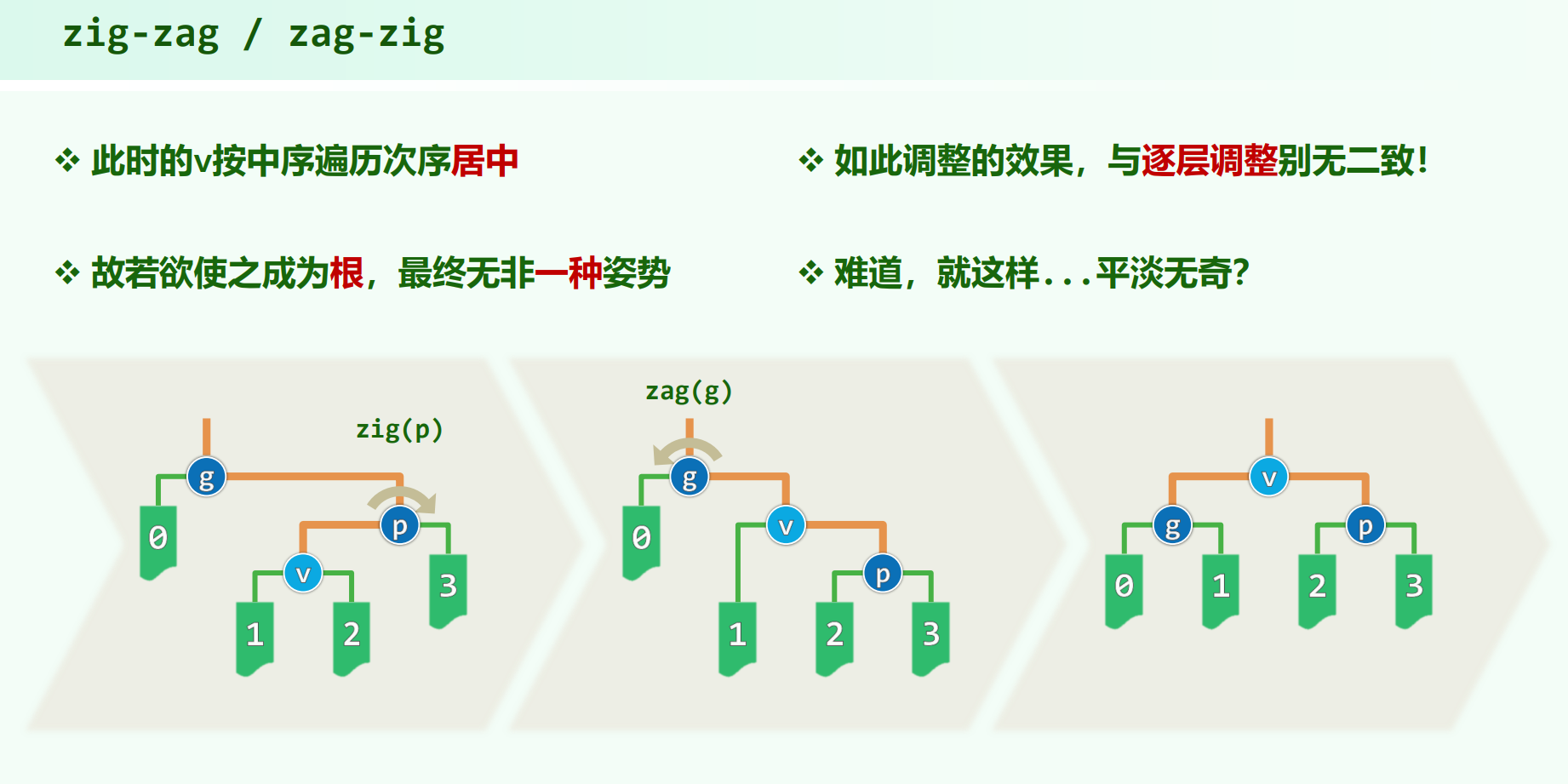
zig-zag / zag-zig
与AVL树的双旋一样
zig-zig / zag-zag
第一步与AVL的单旋一样,在 $\pmb{g}$ 处单旋一次,然后还要再旋一次,把 $v$ 转上去。也就是说和 zig-zag / zag-zig 一样要旋 $2$ 次。
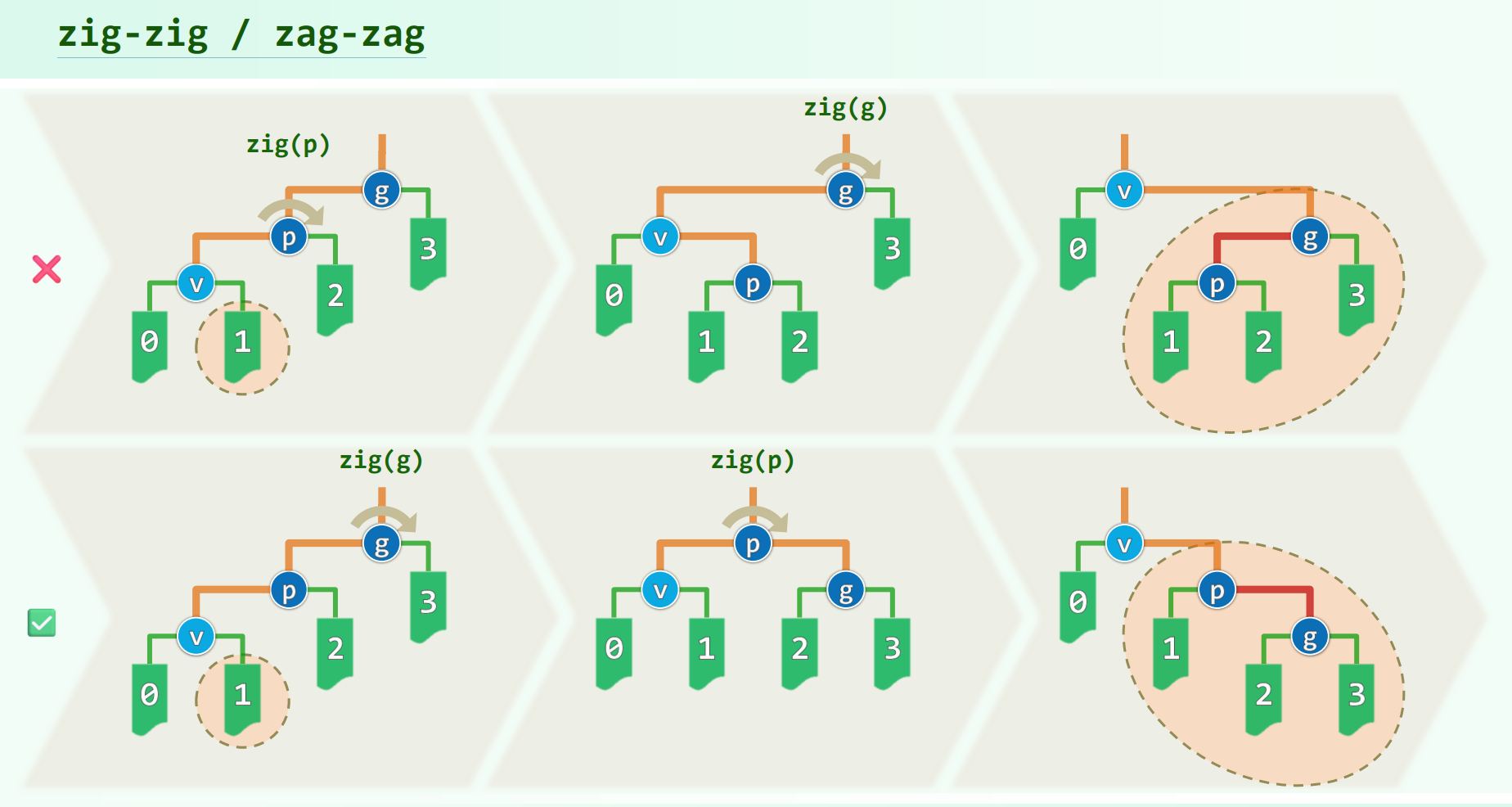
注意这个图里下面的行才是伸展树的双层旋转,上面的行是$v$做了两次逐层旋转。
用单链来看,采用双层伸展,search(1)之后原本到 1 的那条路径长度减半了,不再是单层伸展下长度只减 1 。能避免分摊复杂度为 $O(n)$ 。
习题解析[8−2]: 伸展操作分摊仅需 $O(logn)$ 时间
zig-zag / zag-zig 对单链是怎样的作用?
6
/
1
\ search(3) 3
5 --------> / \
/ 1 6
2 \ /
\ 2 5
4 /
/ 4
3
对这种折线形单链,3的同列都是比自己小的(往下单增),右边那列都是比自己大的(往上单增),search(3)之后其分列3的左右子树。由此可以理解这种情况 zig-zag / zag-zig 也能把路径长度减半。
(不过这种折线形单链怎么操作出来好像不太好说,1 2 3单靠insert是操作不出来这种折线形单链的,最后一个肯定是insert(3),但是 1 2 3 和 2 1 3的结果都不是这种折线形单链。也就是说虽然合法,但是至少单靠insert是操作不出来这种结构的。不过 insert {2 4 1 3}、{4 2 1 3}, delete 4 可以得到 3 lc 1 rc 2 ;insert {2 3 1 4}、{2 4 3 1}、{3 2 1 4}、{3 4 2 1}、{4 2 3 1}、{4 3 2 1}, delete 4 可以得到 1 rc 3 lc 2 的折线形单链。)
补充上面
和研友~聊天,他突然想了这么一种方式:交替插新的最大/最小值,这样能生成这种折线形单链。
以下称:从 $1 \sim n$ 中间开始往两边,对称地交替选取并插入SplayTree 为 min / max 交替插。这么叫是因为每次选出来的值交替地为新的 min / max,即 … max min max min …
具体来说:
-
若有偶数个关键码,例如 1 2 3 4 5 6 7 8 ,按 4 5 3 6 2 7 1 8 / 5 4 6 3 7 2 8 1 的顺序插,一定会出来边从上到下为 左右左右…左 / 右左右左…右 形式的单链(以下称为完美交替)。第一条边往左还是往右看最后插入的值就知道根了。
-
若有奇数个关键码,也一定为单链,但是:
-
如果 n = 3,一定得到左孩子单链 / 右孩子单链
-
如果 n > 3,结果虽仍是单链,但边一定不是完美的 左右左右 / 右左右左 方式,其会是这样的,以 5 4 6 3 7 2 8 1 9 为例(对称选择情况类似):n - 1 为偶数,所以这类例子会先形成 右左右左 形单链,然后插 n 。树根现在为 1 ,边第一步向右,然后向左,这第一个折点就是当前树中的最大值,n 先插在其右孩子,然后旋上去,这个过程是:
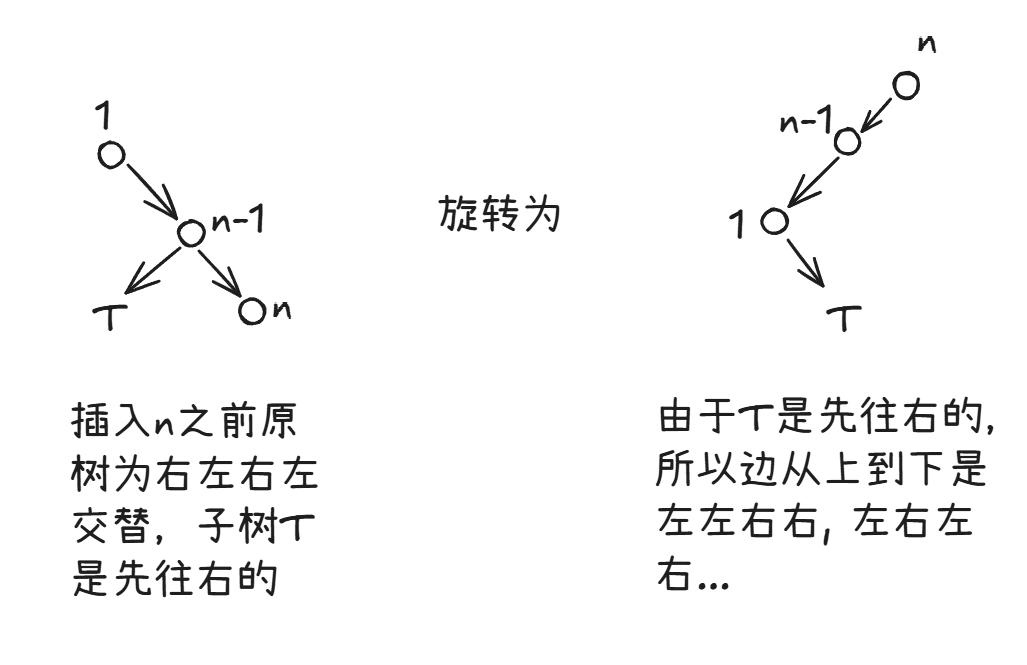
也就是说 n > 3 为奇数的情况会先有 $4$ 条边反常,然后才是完美交替。
-
现在说怎么严格证明case1:n = 2, 4 是符合的,然后对更大的 n ,其可由 case2.2 插入一个 min / max 得到,以上图为例,该在上图的基础上插入一个 0 ,去转一下就知道会变成完美交替。也就是说 n 为奇数 和 n 为偶数 的情况可以交替往前证明。
这里还挺特别,插入 0 之后 0 往上是个 四节点的单方向单链,1 甚至还有右子树,但是转完还是单链。
再看教材P207图8.6,先依次插入 1 ~ n ,然后 Splay::search(1),能保持为单链的 n 最大就为 4 。关于这种左孩子单链,BST::search(1) 的结果规律,看这两个图就能get到了:


以上采取的是直观的插入法(见伸展树的插入),如果采取教材P210的优化插入法,不一定会形成单链。例如 3 4 2 5 1 6 ,使用教材上的优化插法,插入e前会先search(e),将最后被访问的节点提升到根,然后在根位置直接操作插,3 search(3) 4 search(3) 2 search(4) 5 search(2) 1 search(5) 6 ,出来的结果不是单链。
把这个结论记得简洁一点:交替地往SplayTree中插入一个新的最大/最小值,一定会形成单链。
注意必须是交替的 … max min max min … 。不能是 … max max min … 啥的,例如 3 4 5 6 2 1 结果不是单链;也不能说 1 ~ n 从两边往中间选,例如 1 6 2 5 3 4 ,这样是 min max mid mid … ,结果也不是单链。
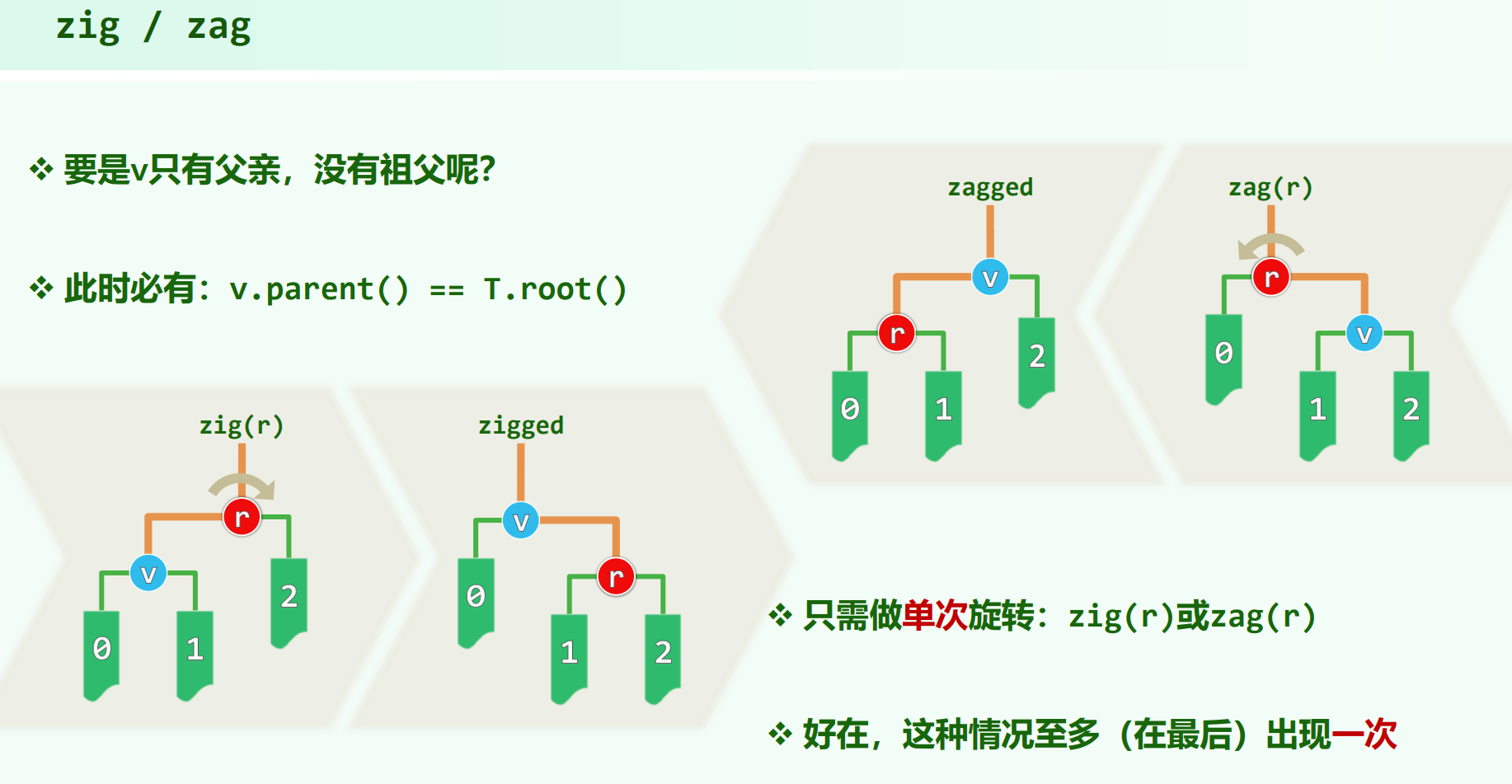
zig / zag
最后可能需要一次单层旋转
伸展树的插入
直观方法是先把节点按二叉搜索树的逻辑BST::search()插入进去,再伸展到根。
但是找节点位置也可以调用Splay::search(),所以:
教材P210 的实现方式是在第一步的search过程中用_hot记录直接前驱/直接后继,然后把直接前驱/直接后继伸展到根(即调用Splay::search(),会把最后被访问的节点转到根),然后把待插入节点直接接到根上。
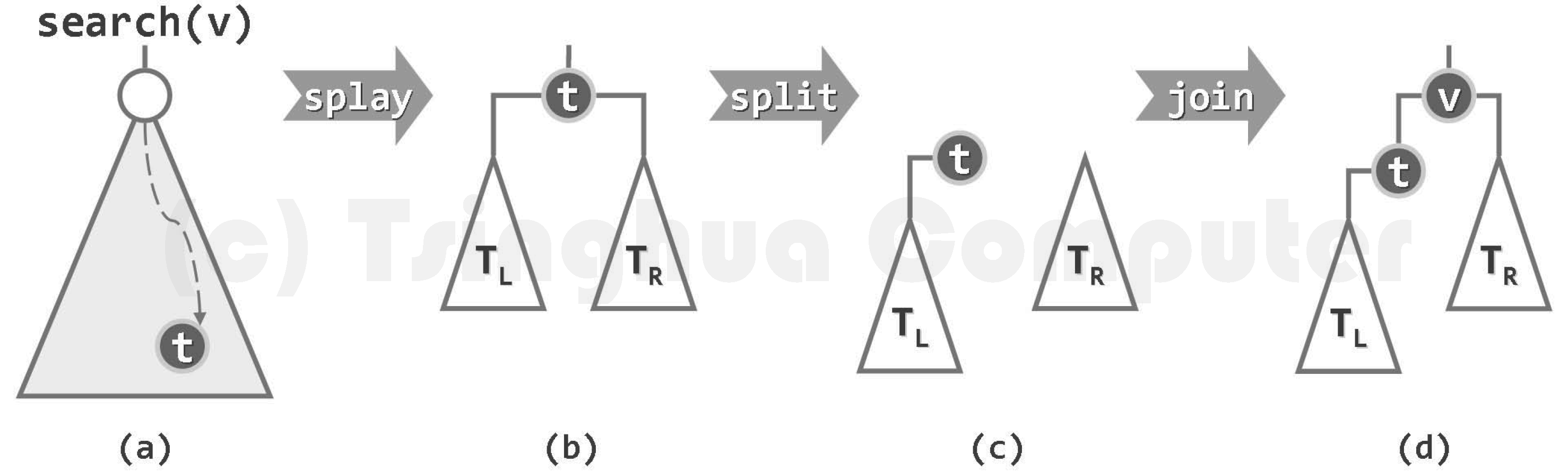
这两种实现得到的树根虽然都是 $v$ ,但是得到的树的结构可能不同。用可视化网站来看(可视化网站上用的是直观方法,调成一步步演示可以看出来):
-
先插入 1 2 3 4 5 6 得到一条单链,然后 Splay::search(1),等价于直观实现的 insert(1)
-
先插入 2 3 4 5 6 得到一条单链,然后 Splay::search(2),再把 1 接到根上,等价于教材中的伸展树插入实现
可以看到结果两棵树有区别。
伸展树的删除
直观方法是先调用BST标准的删除算法,再将_hot伸展至根。
教材P211 的实现方式是先Splay::search(),这样待删除节点就是树根,然后摘除目标节点,用目标节点的直接后继做根(双分支的情况,如果节点是单分支,直接删除根,然后用子树顶替就好)。
综合评价

对伸展树做势能分析
习题解析[8-2]
08.Advanved Search Trees.pdf P25
可以用势能分析法严格证明:伸展树所有基本操作接口的分摊时间复杂度,均为 $O(logn)$
定义势能函数:
\[\Phi(S) = \sum_{v \in S} log|v| ,其中 |v| = 节点 v 的后代数目(包含 v,或者定义为子树 v 的节点规模)\]也就是说单个节点的势能为 $log \lvert v \rvert$ ,树的势能为所有节点势能之和。
叶节点的势能会是 $0$ 。
越平衡/倾侧的树,势能越小/大。
单链:$\Phi(S) = logn! = O(nlogn)$
满树:
\[\begin{align*} \Phi(S) =& \sum_{d = 0}^{h + 1} 2^d \cdot log(1 + 2 + ... + 2^{h + 1 - d}) \\ =& \sum_{d = 0}^{h + 1} 2^d \cdot log(2^{h + 2 - d} - 1) \\ \le& \sum_{d = 0}^{h + 1} 2^d \cdot log(2^{h + 2 - d}) \\ =& \sum_{d = 0}^{h + 1} (h + 2 - d) \cdot 2^d \\ =& (h + 2) \cdot (2^{h + 2} - 1) - \sum_{d = 0}^{h + 1} d \cdot 2^d \\ =& (h + 2) \cdot (2^{h + 2} - 1) - [(h + 1) \cdot 2^{h + 2} - (2^{h + 2} - 2)] \\ =& O(2^h) = O(n) \end{align*}\]设树规模为 $n$ ,访问次数为 $m$ ,且 $m \ge n$
均摊成本 $A_k = T_k + \Phi_{k} - \Phi_{k - 1}$,由上面的计算可知,$\sum \Delta \Phi \le O(nlogn) (可能为负)$,现在只需证明 $\sum A_k = O(mlogn)$ 即可得到 $\sum T_k = \sum A_k - \sum \Delta \Phi = O(mlogn)$ ,从而均摊复杂度为 $O(logn)$
伸展树的一次伸展到根包含多步调整,这里不像双栈当队用到了势能分析法里那样,一次伸展到根的 $A$ 并不是常数,但是仍然可以分析得到:
在对节点 $v$ 的伸展过程中,每一步调整所需均摊成本$A$均不超过 $v$ 的势能变化的 $3$ 倍,即 $3 \cdot [\Phi’(v) - \Phi(v)]$
有了这个结论之后,一次伸展到根的多步调整可以用 $\Delta \Phi(v)$ 来估计,多次伸展到根的操作同样可以用 $\Delta \Phi(v)$ 来估计,$v$ 的始末状态的势能变化不超过 $O(mlogn)$,从而 $\sum A_k = O(mlogn)$ 。
现在分调整操作来分析:
zig / zag
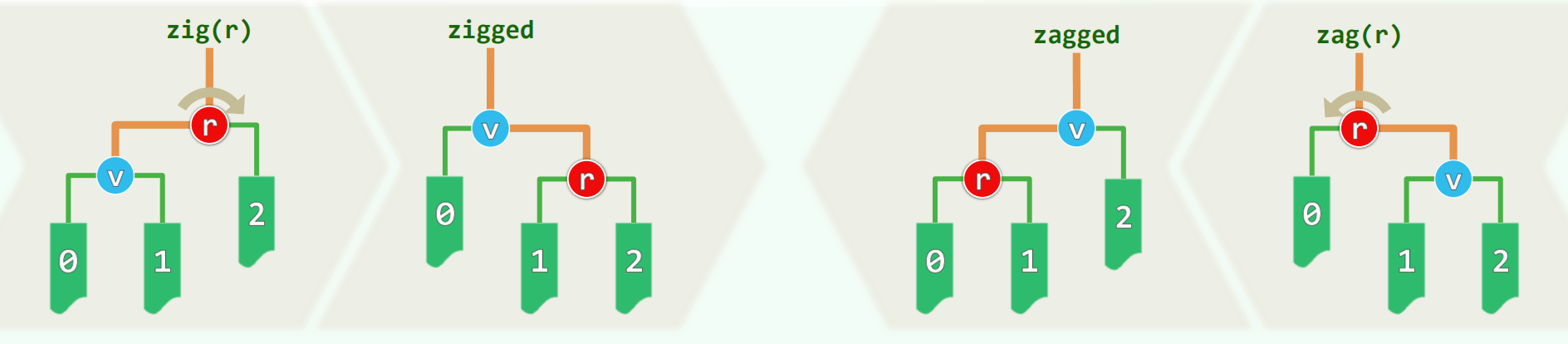
注意这里有个非常关键的 $1$ 是消不掉的,不要认为 $v$ 的后代数一定增加,从而 $\Phi’(v) - \Phi(v) \ge 1$ ,从而 $1 + \Phi’(v) - \Phi(v) \le 2 \cdot [\Phi’(v) - \Phi(v)]$,后代数增加的变化量大于$1$,但是势能是 $log$,$\Phi’(v) - \Phi(v)$ 可能是 0.x ,这里的 $1$ 是消不掉的!
但是好在单层伸展在一次伸展 $v$ 到根的操作中最多只会做 $1$ 次。
zig-zag / zag-zig
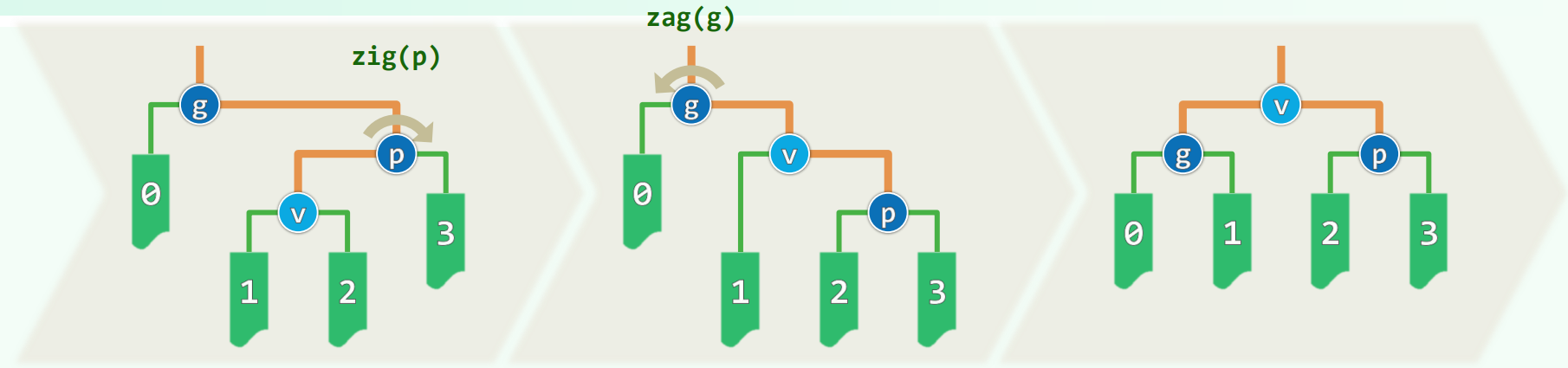
最后一步放大:
由于势函数 $log_2(x)$为凹函数,$\frac{loga + logb}{2} \le log\frac{a + b}{2}$ ,所以 $log \lvert g’ \rvert + log \lvert p’ \rvert \le 2 \cdot (log( \lvert g’ \rvert + \lvert p’ \rvert) - 1) < 2 \cdot (log \lvert v’ \rvert - 1)$ ,即 $\Phi’(g) + \Phi’(p) \le 2 \cdot \Phi’(v) - 2$
zig-zig / zag-zag
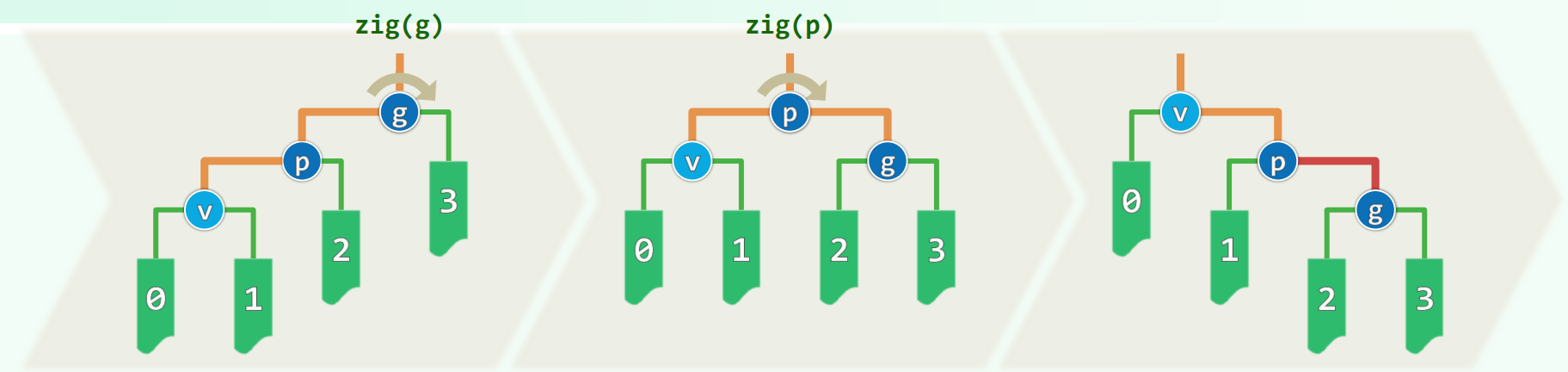
最后一步的放大同样用到了 $logx$ 的凹性,不过这里要选 $v$ 和 $g’$ 两个点,其包含了 $4$ 棵子树和 $v, p$ 两个点,$log \lvert v \rvert + log \lvert g’ \rvert \le 2 \cdot (log(\lvert v \rvert + \lvert g’ \rvert) - 1) < 2 \cdot (log \lvert v’ \rvert - 1)$ ,即 $\Phi(v) + \Phi’(g) < 2 \cdot \Phi’(v) - 2$ 。
综合以上三种情况,一次把 $v$ 旋转到根的所有旋转,其分摊成本加起来为: $A_k \le 1 + 3 \cdot [\Phi(r) - \Phi(v)] \le 1 + 3 \cdot \Phi(r) = O(logn)$,于是 $\sum A_k = O(mlogn)$。
伸展树的基本操作接口的分摊时间复杂度为 $O(logn)$
以上推导没有涉及数的节点变化的情况,但是即使考虑插入和删除操作,分摊复杂度也不会变。以 $m = n$ ,采用直观方法的插入为例,先插入,这步操作的 $A$ 为常数,然后接下来的旋转操作也可以用 $\Delta \Phi(v)$ 来估计,一次伸展到根的过程的 $A = O(log(n + 1))$
回到开始,为什么单层伸展策略不行?
关键在于 zig / zag 的那个 $1$ 消不掉,如果采取单层伸展,一次把 $v$ 伸展到根的过程可能有 $\Theta(n)$ 次单层伸展,$A_k$ 就是 $n + 3 \cdot [\Phi(r) - \Phi(v)]$ ,$\sum A_k$ 会是 $O(n^2)$。
而单层伸展在实际伸展树的调整过程中最多做一次,所以没有问题。
伸展树的性质
-
按单调增顺序插入,结果为左孩子单链,按单调减顺序插入,结果为右孩子单链。
-
再按 原本顺序 / 原本顺序的逆序 访问一遍,会先变成不是单链,最后会回到 原本的单链 / 左右对称且节点顺序相反的单链 。
-
Splay::search(min/max)之后,树根一定会变成单分支(或者叶子)。
这个显然,因为Splay树也是二叉搜索树,另一侧要是非空的话刚刚search的不是min/max了。
-
推论:无论Splay树的当前形态如何,只要按单增/单减顺序访问一遍树中节点,树一定会变成只有左孩子/右孩子的单链。
树中节点值为 {1~n},以按单减顺序访问一遍为例
-
Splay::search(n) 后一定 n 为根,其它节点都在左子树
-
然后search(n - 1),原根的右子树已为只有右孩子的单链。考虑 n - 1 以何种方式与 n 发生旋转。若为 zig,旋转后树根往右保持为向右单链;若为 zag-zig,同理;若为 zig-zig,不可能发生,$v$ 为 n - 1,$g$ 为 n,没有节点可以当 $p$;
也即树根往右始终保持为向右单链,最后Splay::search(1)后左子树为空,整棵树为只有右孩子的单链。
-
-
交替地往SplayTree中插入一个新的最大/最小值,一定会形成单链
见上面