cs
- 10.Graph.pdf
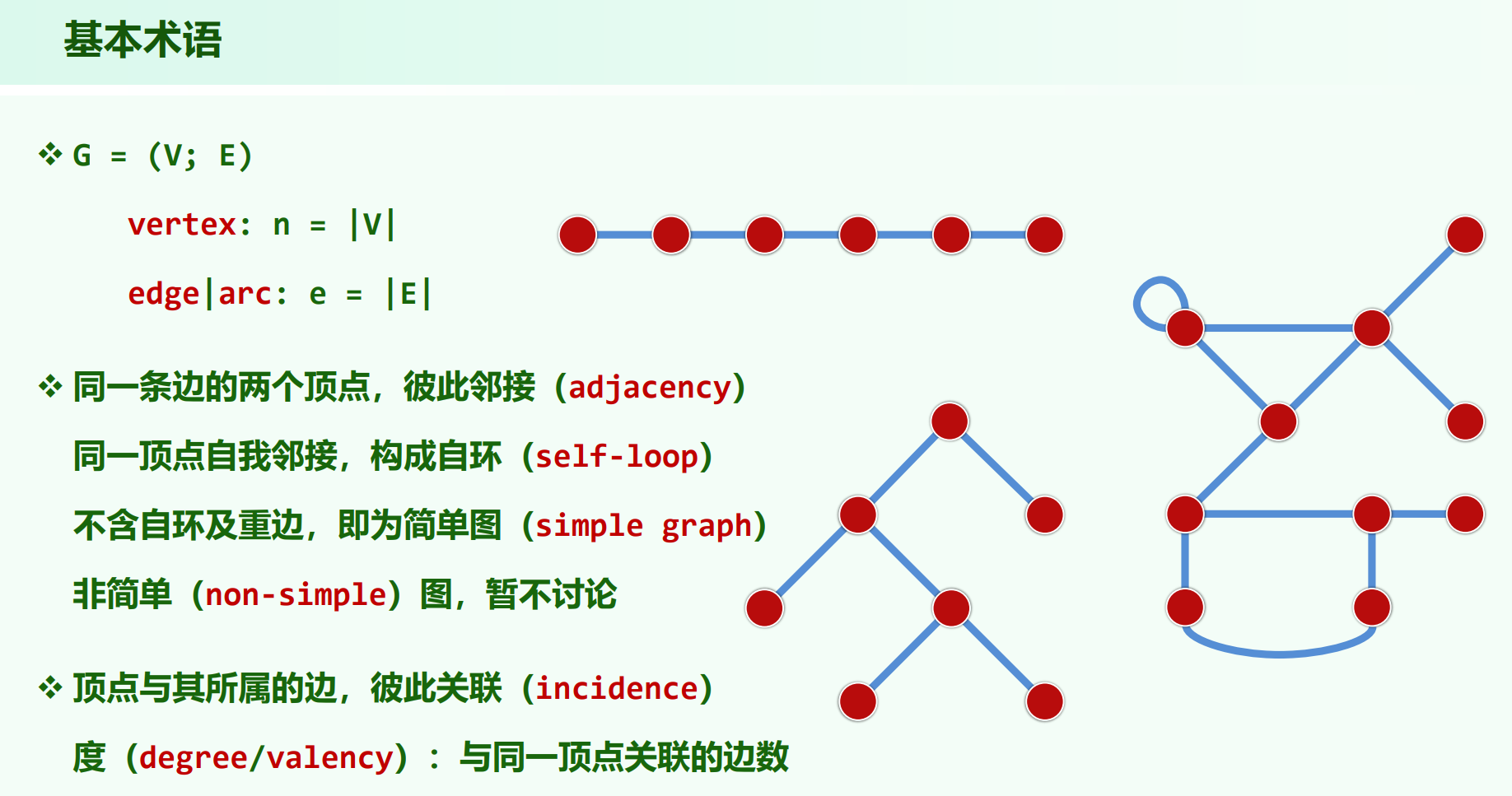
一部分基本概念
bfs
无向图的bfs
性质:
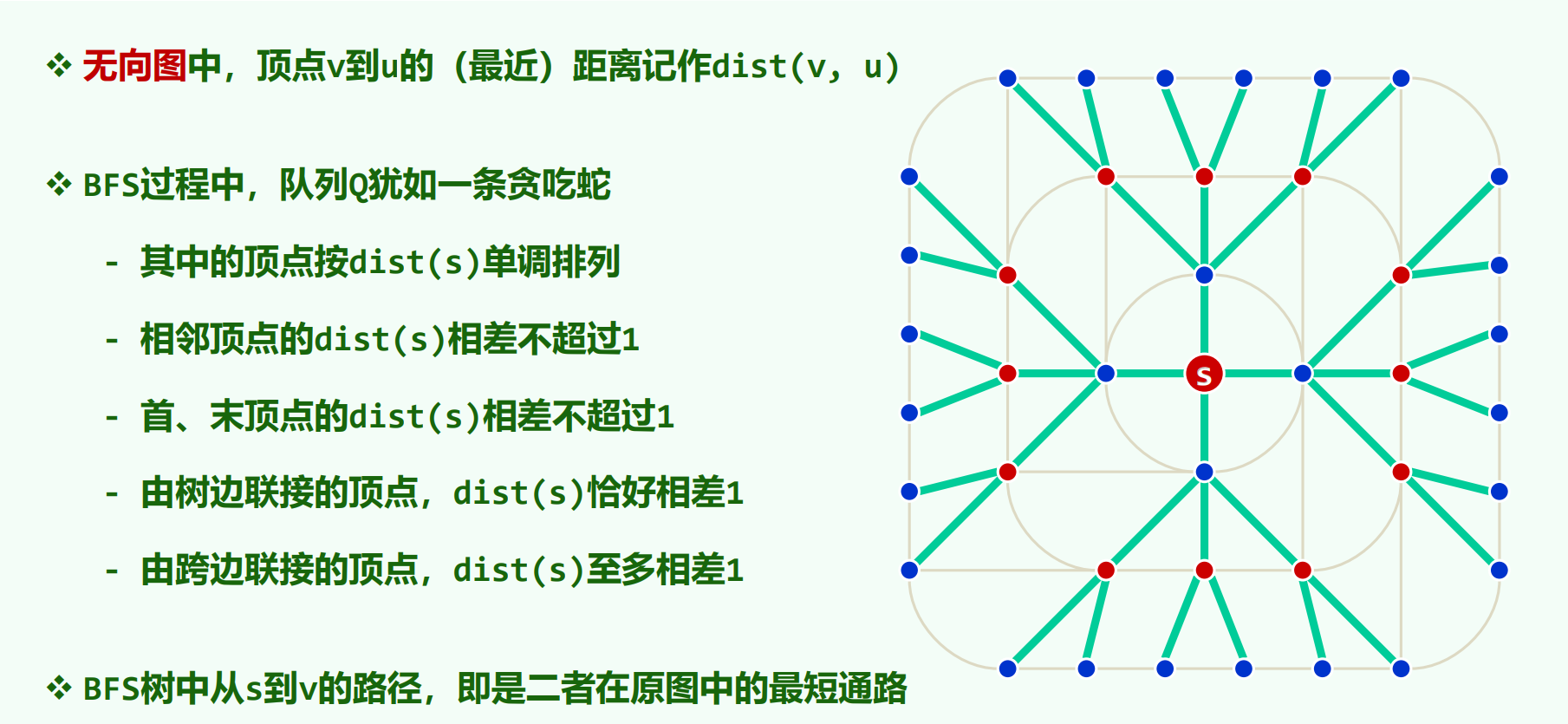
无向图的bfs,当 $v$ 出队去查看邻居 $u$ 时,$u$ 可能是:UNDISCOVERED / DISCOVERED / VISITED 状态。
不过对 bfs , 后两者统一归类称为跨边。
无向图的 bfs 只有树边和跨边。
有向图的bfs
有向图的bfs,当 $v$ 出队去查看邻居 $u$ 时,$u$ 可能是:UNDISCOVERED / DISCOVERED / VISITED 状态。
不过对 bfs , 后两者统一归类称为跨边。
有向图的 bfs 只有树边和跨边。
无向图的dfs
教材P154写了无向图统一把无向边转为两条互逆的有向边,也就是不考虑这种情况?
补充ppt:

但是后面讲的双连通分解又是无向图的 dfs 的情况。
求双连通分量时是无向图的 dfs 的情况,关心的只有树边和后向边,不过前向边也会出现,但不关心,具体看代码。
有向图的dfs
有向图的 dfs 可能出现 树边、前向边、后向边、跨边。
有向图祖先关系的判定:
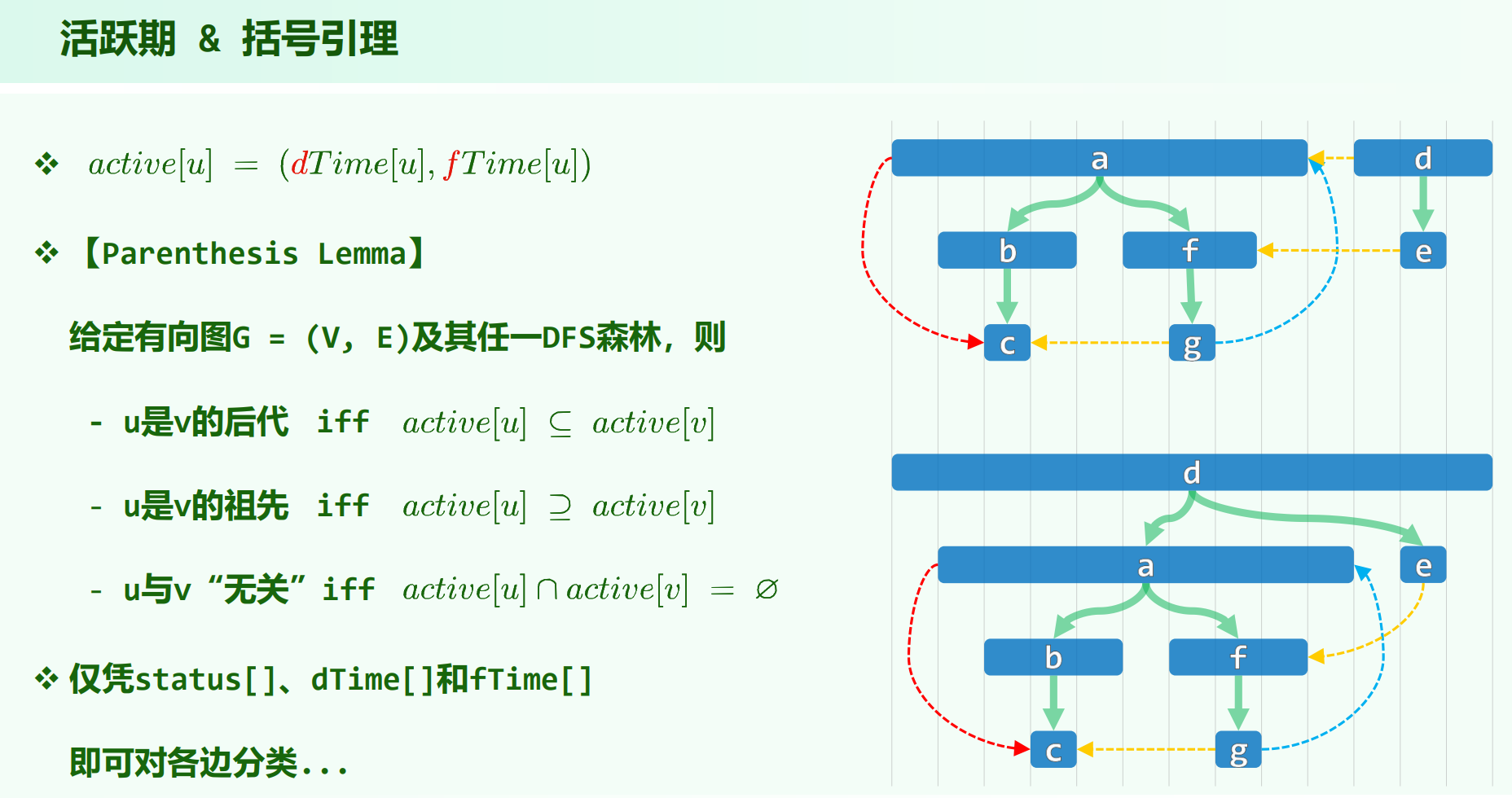
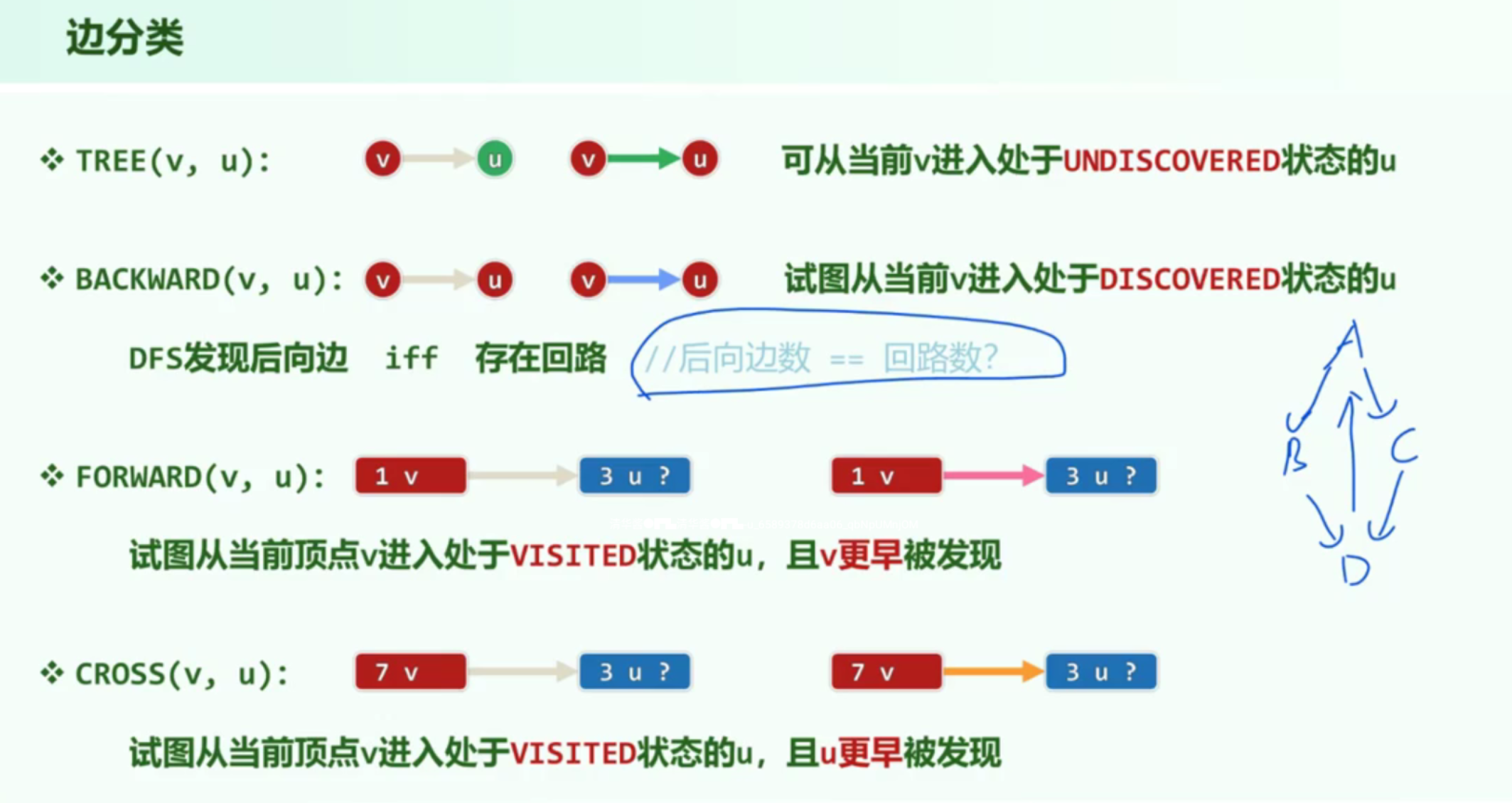
后向边 $\neq$ 环数
dfs发现后向边 iff 存在回路,但是并不能说明回路数。
拓扑排序
有向无环图必存在入度为 $0$ 的节点,也必存在出度为 $0$ 的节点。(否则可以一直走,走 $n$ 步,节点一定有重复,一定有环)
有向无环图 $\Leftrightarrow$ 可拓扑排序
$0$ 入度算法
dfs各顶点被标记为VISITED的顺序为拓扑排序的逆序(逆序输出 $0$ 出度节点)
补充ppt里的一道题:

最短路径
Dijkstra
不能有负权边
生成最短路径树SPT
如果有负权边,无负权环:
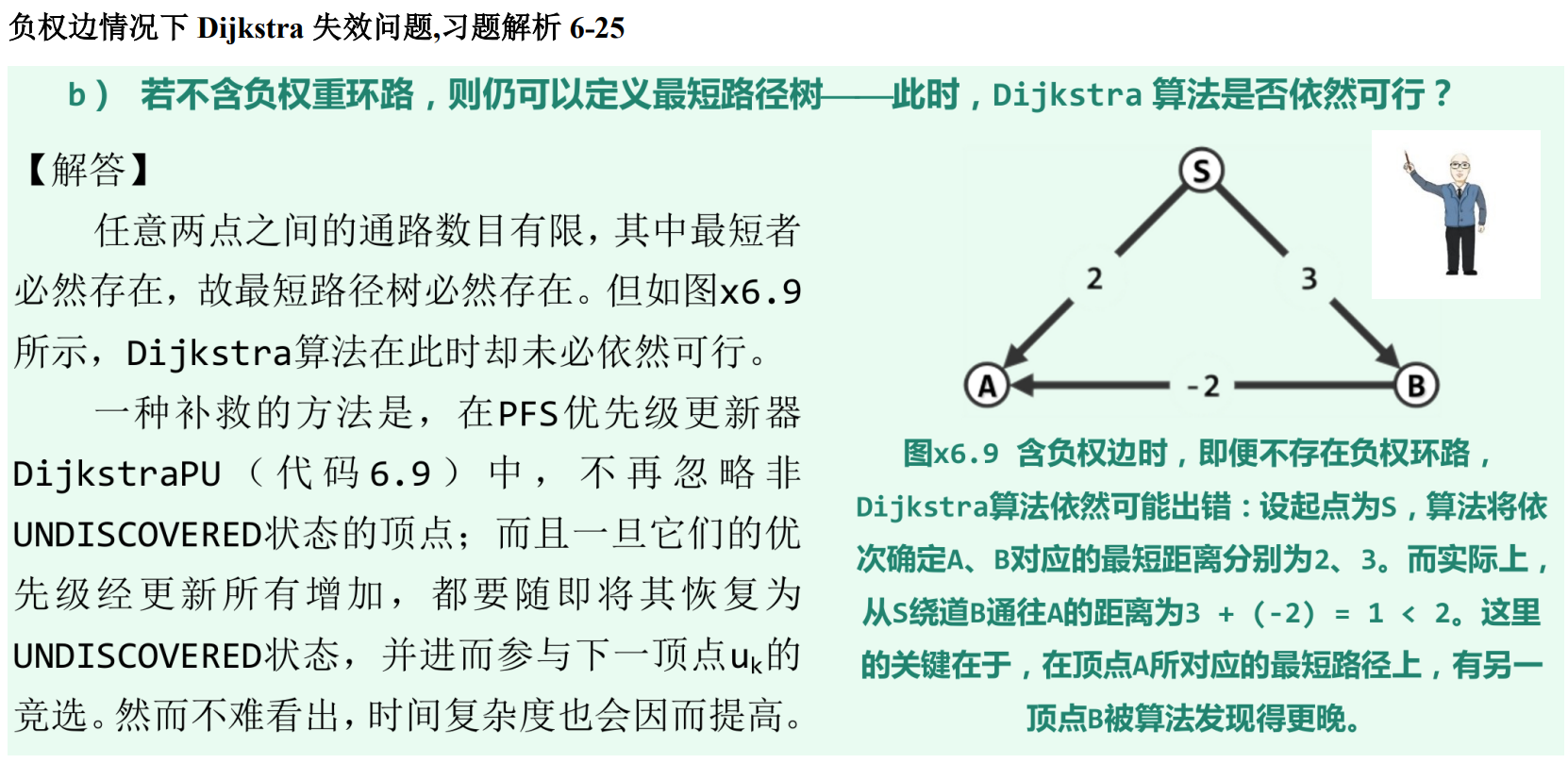 (这个具体coding-practice仓有写)
(这个具体coding-practice仓有写)
Floyd-Warshell
能有负权边,不能有负权环

最小生成树 MST
Prim
和Dijkstra非常像,只是松弛邻居时用边(u, v)的权重,而不是 dis(u) + w(u, v)
有负权边也没问题。
Prim算法的大致思路是:分为已经连通的点集 $S$ 和剩余点集 $U - S$ ,第一个起点要和其它节点连通,选极短跨越边,然后起点加入 $S$ ;$S$ 要和 $U - S$ 连通,选 $S$ 和 $U - S$ 的极短跨越边,这样又连通了一个节点进 $S$ ,然后重复这个过程直到 $S$ 包含所有点。
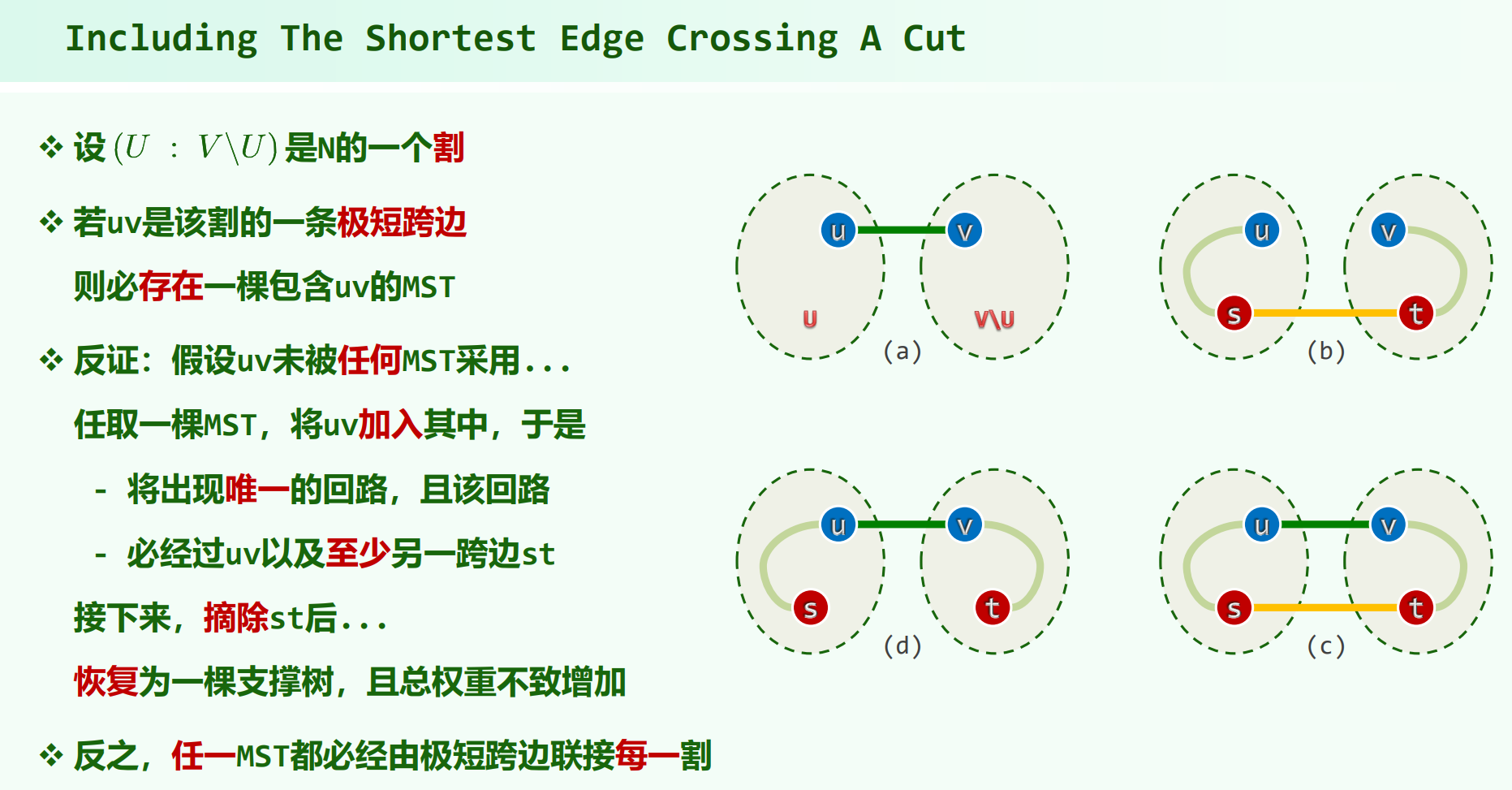
极短跨越边一定都属于某棵最小生成树。(任一极短跨越边都一定存在某棵包含它的最小生成树)
最小生成树的每一边都一定是(某个割的)极短跨越边。
证明:如果某条边不是,则删除最小生成树里的这条边,树形成两个连通分量,二者的节点集形成图的一个割,由反证假设,删掉的边非此割的极短跨越边,则此割的极短跨越边另有其人且权值更小,则选这个极小跨越边即可生成更优的最小生成树。
或者教材P176:“最小生成树总是会采用联结每一割的最短跨越边”
习题解析[6-27]:即使某棵生成树 T 的每一条边都是 G 某一割的极短跨越边,T 也未必是 G 的最小生成树。
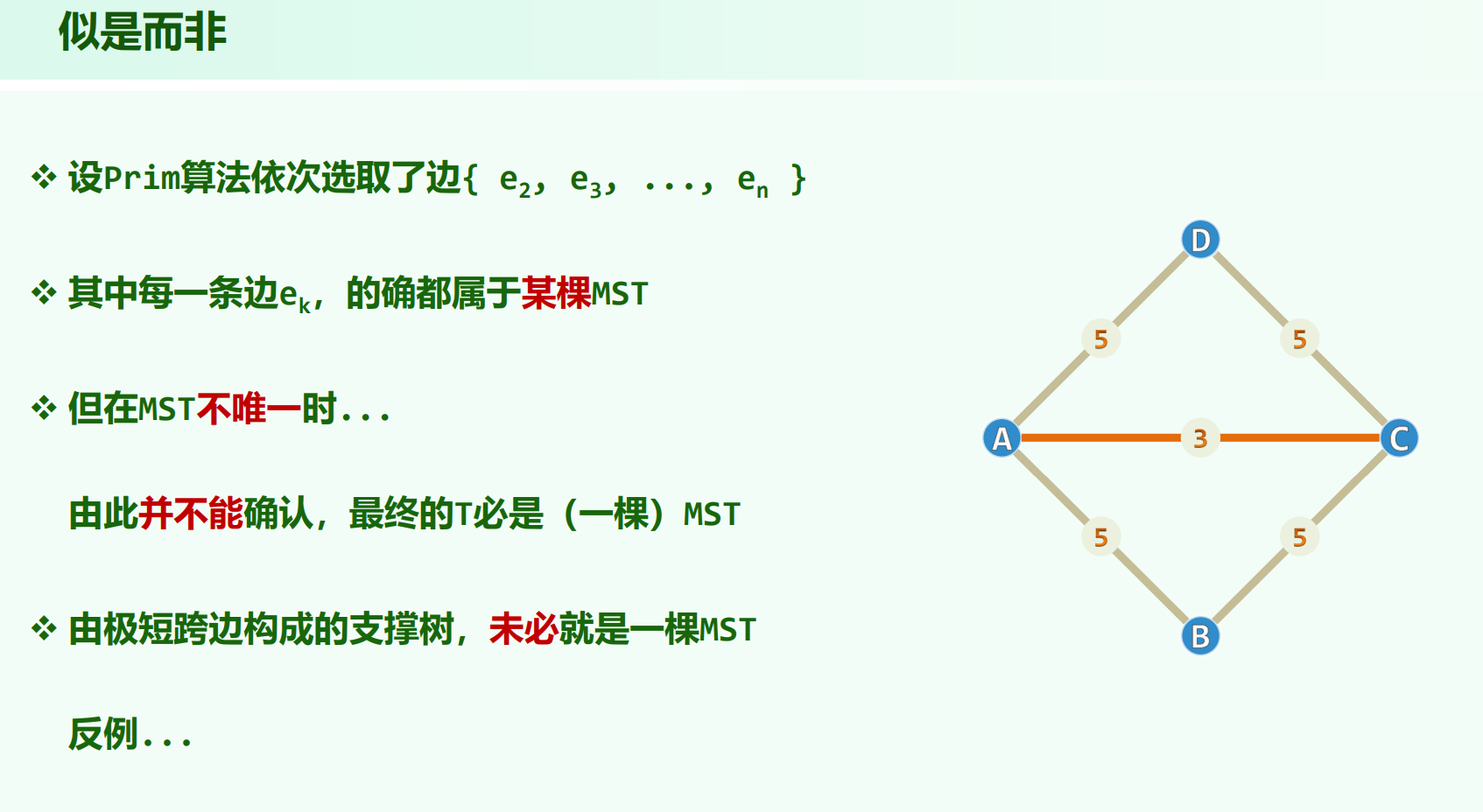
这个图里每条边都是极短跨边,但是选AD、DC、CB构成生成树的话却不是最小生成树。
如果MST唯一,则由极短跨边构成的生成树一定是一棵MST了。因为若除了唯一的这棵MST之外若还有其它极短跨边,则以那条极短跨边的端点为起点跑Prim,会得到另外一棵MST,矛盾。所以,MST唯一的话,极短跨边只有MST的这 $n - 1$ 条边。或者说若有 $n$ 条极短跨边,则至少有两棵MST。
图有多个MST,选 $n - 1$ 条极短跨边组合,未必是MST ;MST唯一,只有那 $n - 1$ 条极短跨边,怎么选都会选成MST。
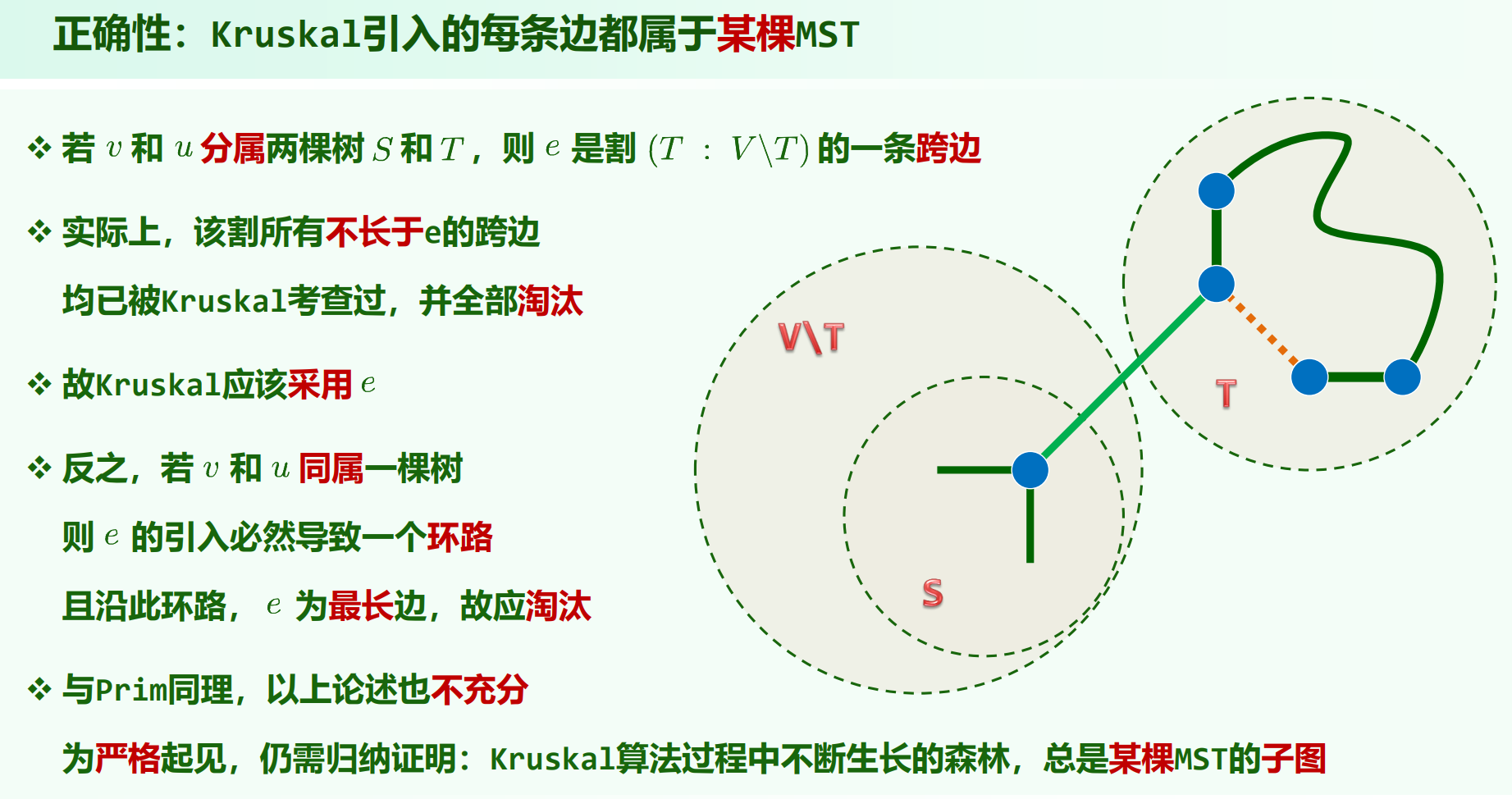
Kruskal
用并查集,不断选两端点不在同一集合的最小边。如果当前候选边的两个节点在同一集合(Kruskal中,并查集的每一分量为一棵树),则加这条候选边会导致成环。
有负权边也没问题。
最小生成树一定包含最短边和次短边
先说明一点,由于边的权值可能相等,例如 $1_1, 1_2, 1_3, 2_1$ ,所以这里最短边和次短边的含义是 ${1_1, 1_2, 1_3}$ 任其二都可以认为是最短边和次短边。
假如MST不包含最短边 $(u, v)$ ,考虑节点 $u$, $v$ 在最小生成树中的情况,选一个点作为根,$u, v$ 在 $lca(u, v)$ 所在的子树中,现在把最短边 $(u, v)$ 加进来,然后必定成环,但是只需删除环上的一条边即可。
MST也一定包含次短边,如果次短边在别的子树,同理操作即可,若还在这棵子树,也总可以操作出来。
但是,再次短者则未必,因为可能无法避免地与最短边和次短边构成环。
简洁一点的结论是:如果图的边权互不相同,则最小生成树一定包含最短边和次短边。(用Kruskal算法的过程很容易看出来)