cs
- 09.Dictionary.pdf P22
除余法

这里我理解选 $M$ 为素数,还有个理由是,如果 $M$ 为合数,$hash = key \% M$,则 $hash$ 一定是 $gcd(key, M)$ 的倍数。因为:
\[N = kM + r,N = ng,M = mg,then: \\ \frac{r}{g} = n - km \\ 右边是整数,则左边也是整数\]既然 $r$ 一定为 $g$ 的倍数,说明不是每个值都能 $\%$ 出来,不如让 $M$ 为素数,则 $g = 1$。
几个算法导论中的结论

算法导论P154定理11.6:

这个结论是个上界,证明过程中放大了,其实是放成了每步成功率都是 $1 - \alpha$ 的几何分布。
另外几个结论:



重散列 (Rehashing)
装填因子要算上懒惰删除(和教材上代码不一样)

平方探测

以上图中假定了 $M > 2$ ,如果 $M = 2$ 的话会发现不符合。
现在来证明这个结论:
若 $M$ 为奇素数,则 $k^2 \ \% \ M$ 恰有 $\lceil M / 2 \rceil$ 种取值,且由试探链的前 $\lceil M / 2 \rceil$ 项取遍。
$\% M$ 的结果有 ${0, 1, 2, … , M - 1}$ 共 $M$ 种,探测时是计算 $hash(key) + k^2 \ \% \ M$ ,$hash(key)$ 不变,只需考虑 $k^2 \% M$ 的结果就行了,这个映射为:
\[\{0^2, 1^2, 2^2, ...\} \rightarrow \{0, 1, 2, ... , M - 1\}\]这不一定是个满射,所以要考虑其像。由取模的性质 $k * k \ mod \ M = (k \ mod \ M) * (k \ mod \ M) \ mod \ M$ ,所以只需考虑一个长为 $M$ 的周期的像就行了,即:
\[\{0^2, 1^2, 2^2, ... , (M - 1)^2\} \overset{\% M}\rightarrow \{0, 1, 2, ... , M - 1\}\]后面的一定算出来的是和前面重复的位置。
若有两个不同位置 $a$ 和 $b$ $(0 \le a, b \le p - 1)$ 使得 $a^2 \equiv b^2 \ (mod \ p)$ ,则 $(a + b)(a - b) \equiv 0 \ (mod \ p)$ ,由于 $p$ 是素数,只能 $(a + b) \equiv p$ 或者 $(a - b) \equiv p$ ,后者不可能,只能 $a + b \equiv p$ 。
也就是说
\[\{0^2, 1^2, 2^2, ... , (M - 1)^2\} \overset{\% M}\rightarrow \{0, 1, 2, ... , M - 1\}\]这个映射的特点是,当且仅当 $a + b = M$ 时,映射到同一个数。除了 $0$ 没有对称点,其它数都有对称点。所以,$0$ 、${1, M - 1}$ 、${2, M - 2}$ … 分别映射到一个数。
($M$ 为奇数) ${0^2, 1^2, 2^2, … , (\frac{M-1}{2})^2}$ 就取遍了所有映射结果,共 $\lceil \frac{M}{2} \rceil$ 个像值。
${k^2}$ 这个序列在$[0, \frac{M-1}{2}]$就不重复地取遍了所有二次剩余,后面就都是在重复了。
结论:对于一个奇素数 $p$ ,模 $p$ 的非零二次剩余个数为 $\frac{p - 1}{2}$ ,二次剩余个数为 $\frac{p + 1}{2}$ ,非二次剩余个数为 $\frac{p - 1}{2}$ 。 ( $0$ 一定为二次剩余,因为 $0^2 \equiv 0 \ (mod \ p)$ )
对于 $p = 2$ ,$0, 1$ 都是二次剩余。
解释:
二次剩余的“剩余”原文是 residue ,含义上感觉更像“二次余数”。表示模 $p$ 的余数 ${0, 1, … , p - 1}$ 中,哪些余数是完全平方数,即可以找到一个 $k^2$ 映射到它。
但是,按概念来说,$4^2 \equiv 2 \ (mod \ 7)$,那么也有 $4^2 \equiv 2 + 7k \ (mod \ 7)$,$2 + 7k$ 都是“模 $p$ 意义下的完全平方数”。
所以,这里的“模 $p$ 的二次剩余个数”更确切地说是指“二次剩余类”的个数,或者说特指 $[0, p - 1]$ 范围内的“二次余数”。
费马二平方和定理
参考:
一个奇素数 $p$ 可以表示为两个整数的平方和,即 $p = a^2 + b^2$ (其中a, b为整数),当且仅当这个素数满足 $p \equiv 1 \ (mod \ 4)$
偶素数只有 $2$ 一个,其也可以,$2 = 1^2 + 1^2$ 。
注意前提是 $p$ 为素数,然后:$p$ 可以写成二平方和 $\iff$ 其是 $4k + 1$ 形式。
$2021$ 是 $4k + 1$ 的形式,但是其为合数 $2021 = 43 * 47$ ,写代码试下就会发现其不能写成二平方和。$2025$ 也是 $4k + 1$ 形式的合数,但是 $2025 = 0^2 + 45^2 = 27^2 + 36^2$
不过如果是 $4k + 3$ 的形式,无论是质数还是合数,其都不能写成二平方和。如果可以,即有 $4k+3 = a^2 + b^2$ 的话,两边 $mod \ 4$,左边一定为 $3$ ;右边,一个数模 $4$ 的可能为 $0,1,2,3$,然后平方后是 $0,1$,然后两个这样的相加,可能为 $0,1,2$,不可能为 $3$ 。
更一般的结论
参考:
-
deepseek的回答
一个大于 1 的正整数 $n$ 可以表示为两个整数的平方和,当且仅当 $n$ 的所有形如 $4k + 3$ 的质因子的幂均为偶数。
这个定理说明了,任意一个数(不一定为素数了)如果想要能表示成二平方和,要看其素因子,$4k + 1$ 形式的素因子没干扰,剩下的素因子只有 $4k + 3$ 的形式,每个这类素因子的指数都得是偶数。
($4k$ 不会是素因子,$4k + 2$ 为素因子只能是其为 $2$ 的时候,后面会看到由于 $2$ 能写成二平方和 $1^2 + 1^2$,不会影响结论)
证明:
先证必要性:如果 $n$ 可表示为二平方和,则所有 $4k+3$ 型素因数的指数为偶数。
先证一个引理:$n$ 为一个二平方和素数,即 $n$ 可写为 $a^2 + b^2$ ,$p$ 为一个 $4k + 3$ 型素数且 $p \mid n$ (即 $p$ 为 $n$ 的任一个 $4k + 3$ 型素因子),则:$p \mid a$ 且 $p \mid b$ 。
证明:
由于 $p \mid n$,则 $a^2 + b^2 \equiv 0 \ (mod \ p)$ ,如果 $p \nmid a$,由费马小定理可知 $a$ 有逆元且逆元 $a^{-1} = a^{p - 2}$ ,两边乘这个逆元,得到 $1 + (b \cdot a^{-1})^2 \equiv 0 \ (mod \ p)$ ,即 $(b \cdot a^{-1})^2 \equiv -1 \ (mod \ p)$。这说明在模 $p$ 意义下,$-1$ 是二次剩余。
$a$ 为 模数 $p$ 的二次剩余的含义是:$a$ 可由某个数 $x$ 的平方得到,即存在 $x$ 使得 $x^2 \equiv a \ (mod \ p)$
而由欧拉判别法:$(-1)^\frac{p-1}{2} = (-1)^\frac{4k+3-1}{2} = (-1)^{2k+1} \equiv -1 \ (mod \ p)$
$-1$ 经欧拉判别法算出来的结果为 $-1$ ,说明 $-1$ 不是 $p$ 的二次剩余。矛盾,说明 $p \mid a$。同理可得 $p \mid b$ 。
引理证明完毕。
由引理,$n$ 的素因子 $p$ 满足 $p \mid a$ 且 $p \mid b$ ,所以 $p^2 \mid a^2$ 且 $p^2 \mid b^2$ ,从而 $p^2 \mid (a^2 + b^2)$,这意味着:
若 $n$ 可表示为二平方和,$p$ 为 $n$ 的一个 $4k + 3$ 型素因子,则 $n$ 一定可以整除掉 $p^2$ ,质因子 $p$ 的指数一定 $\ge 2$。
而 $a = p \cdot a_1, b = p \cdot b_1$ ,则 $n / p^2 = a_1^2 + a_2^2$,仍然是一个二平方数,且 $n / p^2$ 的质因数分解中 $p$ 的指数减 $2$ 了,如果 $p$ 的指数还有剩,则一定 $\ge 2$,重复这个过程即可知:$p$ 的指数一开始必定为偶数,必要性成立。
再证充分性:如果所有 $4k + 3$ 型素因数的指数为偶数,则 $n$ 可表示为二平方和。
考虑 $n$ 的素因子,要么是 $2$ ,要么是 $4k + 1$ 型,要么是 $4k + 3$ 型。如果是 $2$ ,$2 = 1^2 + 1^2$ ,可以写为二平方和 ; 如果是 $4k + 1$ 型,由费马二平方和定理,其一定可以写为二平方和。由Brahmagupta–Fibonacci identity:$(a^2 + b^2)(c^2 + d^2) = (ac - bd)^2 + (ad + bc)^2 = (ac + bd)^2 + (ad - bc)^2$ 。这个婆罗摩笈多-斐波那契恒等式意味着二平方和相乘可以化为二平方和。用这个等式处理,所有 $2$ 和 $4k + 1$ 型素因子的部分可以化为单个二平方和。
对于剩下的 $4k + 3$ 型素因子,由于其指数一定全为偶数,则利用 $p^2 \cdot (a^2 + b^2) = (pa)^2 + (pb)^2$ ,也可以化为二平方和。
于是,$n$ 可以化为二平方和,充分性成立。
双平方探测
参考:
-
习题解析[9-17]
-
deepseek的回答
习题解析[9-17]的结论:双平方探测的查找链 ${0, 1^2, -1^2, 2^2, -2^2, 3^2, -3^2, … }$,当散列表长取 $4k + 3$ 型素数时,一定有:任一关键码所对应的查找链,前 $M$ 个桶必然互异(也即恰好遍取整个散列表)。
由上面的结论:
${0^2, 1^2, 2^2, … , (\frac{M-1}{2})^2} \ mod \ M$ 的结果各不相同。同理,${0^2, -1^2, -2^2, … , -(\frac{M-1}{2})^2} \ mod \ M$ 的结果也各不相同。
二者有一个 $0$ 是相同的,现在证明:
${1^2, 2^2, … , (\frac{M-1}{2})^2} \ mod \ M$ 和 ${-1^2, -2^2, … , -(\frac{M-1}{2})^2} \ mod \ M$ 的结果也互不相同。
假设存在 $a^2 \equiv -b^2 \ (mod \ M)$,(a, b分属两类),则:
$a^2 + b^2 \equiv 0 \ (mod \ M)$,记 $n = a^2 + b^2$ ($n > 0$),$n$ 为 $M$ 的倍数,说明 $M$ 为 $n$ 的素因子,而既然 $n$ 可写为二平方和,由上面的结论,$M$ 这个 $4k + 3$ 型素因子的指数必须得是偶数,则 $\ge 2$。
则有 $n \ge M^2$ ,但是 $n$ 最大为 $(\frac{M-1}{2})^2 + (\frac{M-1}{2})^2$,不可能。
更二级结论的做法是:
若有 $a^2 + b^2 \equiv 0 \ (mod \ M)$,$b$ 不会是 $M$ 的倍数,同样,由费马小定理得 $b$ 的逆元 $b^{-1} = b^{M - 2}$,乘 $b^{-1}$,则 $(a \cdot b^{-1})^2 \equiv -1 \ (mod \ M)$ ,这说明 $-1$ 是 $M$ 的二次剩余。
但由欧拉判别法,$(-1)^\frac{M-1}{2} = (-1)^\frac{4k+3-1}{2} = (-1)^{2k+1} \equiv -1 \ (mod \ M)$,$-1$ 又不是 $M$ 的二次剩余。矛盾,所以 $a^2 + b^2 \equiv 0 \ (mod \ M)$ 不存在。
上面的结论不是说二次剩余(类)恰有 $\frac{M + 1}{2}$ 个吗?为什么这里能探查 $M$ 个桶?
实际上,这里的本质是 ${k^2, k \ge 0}$ 映射到了二次剩余(类),${-k^2, k > 0}$ 映射到了非二次剩余(类)。由于 $M = 4k + 3$ 时 $-1$ 不是二次剩余,则 ${-k^2, k > 0}$ 也不是二次剩余,否则若有 $-k^2 \equiv a \ (mod \ M)$,两边乘 $-a^{-1}$,$-1$ 变二次剩余了。所以这里能探到的桶个数为:0 + 非零二次剩余 + 非二次剩余 = $1 + \frac{M - 1}{2} + \frac{M - 1}{2} = M$ 。
$二次剩余 × 二次剩余 = 二次剩余$
$二次剩余 × 非二次剩余 = 非二次剩余$
$非二次剩余 × 非二次剩余 = 二次剩余$ (用欧拉判别法证)
双平方探测,散列表长 $M$ 为 $4k + 1$ 型素数会怎么样?
结论:${1^2, 2^2, … , (\frac{M-1}{2})^2} \ mod \ M$ 和 ${-1^2, -2^2, … , -(\frac{M-1}{2})^2} \ mod \ M$ 探测到的位置是重复的。记两个序列的探查位置分别为 $S$ 和 $S’$,其内部各自不重复。现证这两个集合相等。
因为 $M = 4k + 1$ 时,$(-1)^\frac{M-1}{2} = 1$ ,$-1$ 是二次剩余。存在 $t$ 使得 $t^2 \equiv -1 \ (mod \ M)$
则 $-k^2 \equiv t^2 k^2 \equiv (tk)^2 \ (mod \ M)$,则 $-k^2 mod \ M$ 的结果也是二次剩余,或者说 $-k^2$ 也对应一个二次剩余(或者用 二次剩余 × 二次剩余 = 二次剩余 的结论)。$S$ 和 $S’$ 内部各自不重复,$S$ 为二次剩余集合,而 $S’$ 也是二次剩余集合。$M = 4k + 1$ 时取负运算把二次剩余集合映到自身上(是一个置换),这种情况取负是封闭的。
例如 $M = 13$,0 1² 2² 3² 4² 5² 6² 模13分别为 0 1 4 9 3 12 10,-1² -2² -3² -4² -5² -6² 模13分别为 12 9 4 10 1 3 。
题目
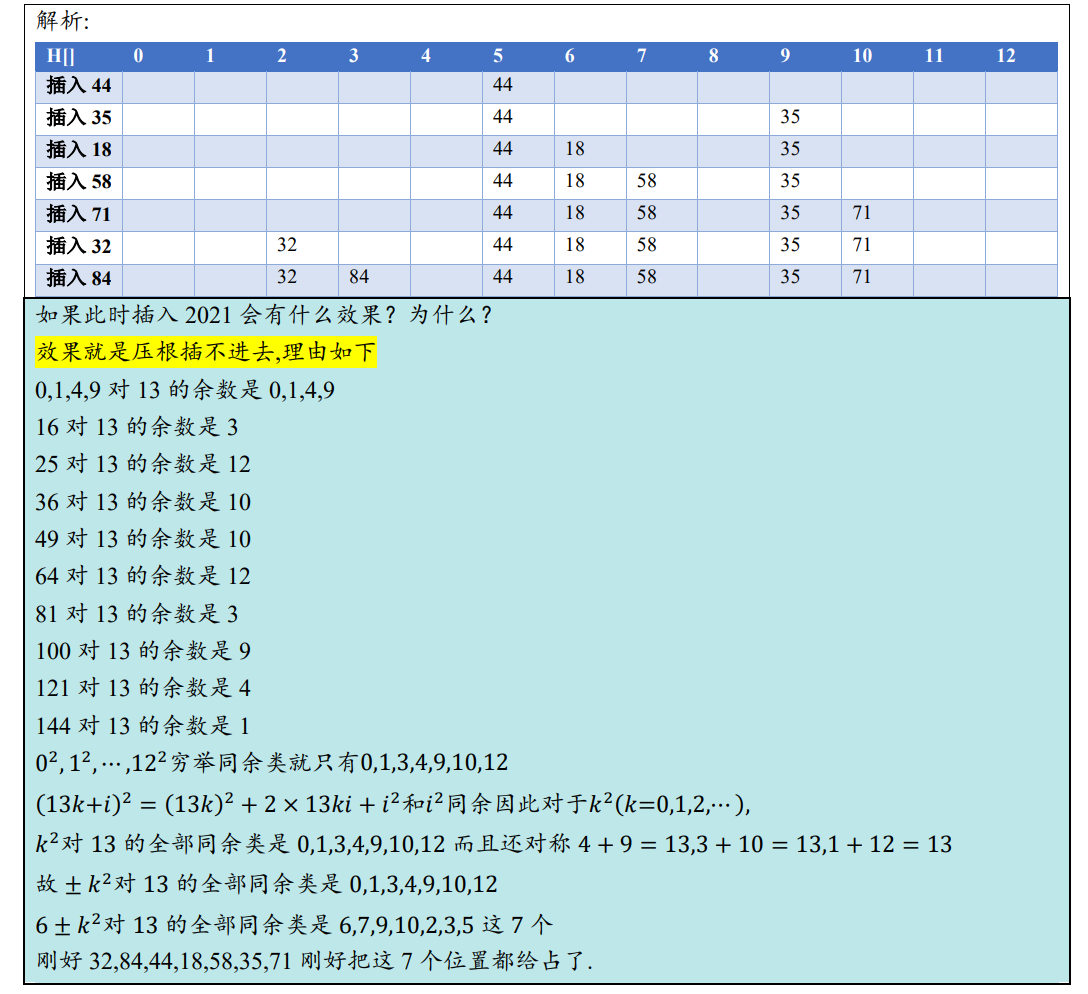
$M = 4k + 1$ 情况下的双平方探测,上面有结论,威哥的解答是不依赖背景的解答。

$a_0$ 和 $b_0$ 是公共的,但是这里 $2021 = 43 * 47$ 不是质数,上面的一些结论用不了。只能用这个,考虑 $a_i = b_j$ ,如果 $j = 0$ ,则对应的 $a_j = b_j = 0$ ,就是 $a_0$ 和 $b_0$ 的情况 ;否则 $a_j = b_j = 2021 - a_j$ ,$a_i + a_j = 2021$ ,$2021$ 的两个素因子都是 $4k + 3$ 型,但是指数为奇数,所以一定不能写成二平方和。只有 $a_0$ 和 $b_0$ 是公共的,答案为 $1$ 。